ASE Basics

The Atomic Simulation Environment (ASE) is a useful OSS library for advancing atomistic simulations in Python. In this section, we will introduce the basic usage of ASE.

• Documentation: https://wiki.fysik.dtu.dk/ase/

• gitlab: https://gitlab.com/ase/ase

Atoms

In ASE, the Atoms class represents systems made up of multiple atoms.

• https://wiki.fysik.dtu.dk/ase/ase/atoms.html

The Atoms class holds the following attribute (variable) to represent the structure required for atomistic simulation, as described in the previous section.

• Element type of each atom

• Coordinate value

• Velocity (momentum)

• Cell

• Periodic boundary conditions, etc.

How to create Atoms: Specify element and coordinates directly

The most primitive way to create Atoms is to directly specify the elements and their coordinates. The following is an example of creating a hydrogen molecule, H2, with the first H at the xyz coordinate value [0, 0, 0] and the second H at the xyz coordinate value [1.0, 0, 0].

from ase import Atoms

atoms = Atoms("H2", [[0, 0, 0], [1.0, 0, 0]])

You can also visualize atoms. Here, we use the view method of ASE and a library called nglviewer to perform the visualization.

You can also interactively manipulate the atomic structure with the mouse while displaying it in 3D with nglviewer. For more information on visualization, see Appendix_1_visualization.ipynb.

from ase.visualize import view
from pfcc_extras.visualize.view import view_ngl

#view(atoms, viewer="ngl")
view_ngl(atoms, representations=["ball+stick"], w=400, h=300)

It is also possible to draw a png image using ASE as shown below.

from ase.io import write
from IPython.display import Image

write("output/H2.png", atoms, rotation="0x,0y,0z", scale=100)
Image(url='output/H2.png', width=150)

The following is a utility method that allows the above program to be done in one line. We will use it from now on.

from pfcc_extras.visualize.ase import view_ase_atoms

view_ase_atoms(atoms, figsize=(4, 4), title="H2 atoms", scale=100)

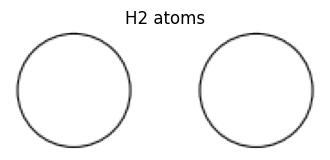
Instead of elemental symbols symbols, atomic numbers can be specified as numbers.

co_atoms = Atoms(numbers=[6, 8], positions=[[0, 0, 0], [1.0, 0, 0]])
view_ngl(co_atoms, representations=["ball+stick"], w=400, h=300)

view_ase_atoms(co_atoms, figsize=(4, 4), title="CO atoms", scale=100)

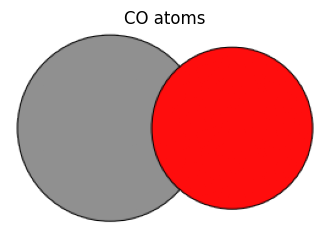
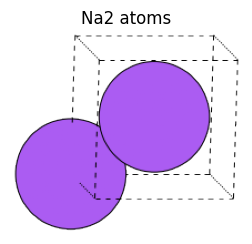
If you want to define a system with periodic boundary conditions, you can specify periodic information in cell and turn on or off whether to apply periodic boundary conditions for each of the a-axis, b-axis, and c-axis in pbc.

from ase import Atoms


na2_atoms = Atoms(
    symbols="Na2",
    positions=[[0, 0, 0], [2.115, 2.115, 2.115]],
    cell=[4.23, 4.23, 4.23],
    pbc=[True, True, True]
)

view_ngl(na2_atoms, w=400, h=300)

view_ase_atoms(na2_atoms, rotation="10x,10y,0z", figsize=(3, 3), title="Na2 atoms", scale=30)

Attribute and method in ASE

The atoms holds information about the structure and can be referenced through the attributes and get_XXX functions. Attributes are variables that the Atoms class possesses, some of which can be referenced directly as atoms.xxx.

Some information can be accessed through methods. The following is a summary of the return values (what the shape looks like as a numpy array) of the main attribute and methods.

• Attribute

  • symbols: returns a summary of elemental species and their numbers.

  • numbers: array of atomic numbers, shape is (N,).

  • positions: the coordinates of each atom, shape is (N, 3) where 3 means xyz coordinates.

  • cell: represented by the Cell class of ASE.

    • The details of the Cell class are described later. In general, it is represented by a (3, 3) matrix of vectors of the a, b, and c axes respectively, for example in triclinic crystal. In some cases like orthorhombic crystal, cell can be represented by a (3,) shape vector, which represents the length of a, b, and c axes.

  • pbc: Indicates whether there is a periodic boundary condition in each direction.

• Method

  • get_masses(): returns the mass of each atom.

  • get_momenta(): return the momentum for each atom.

  • len(atoms): returns the number of atoms N in the whole atoms.

print(f"symbols  : {atoms.symbols}")
print(f"positions: {atoms.positions}")
print(f"cell     : {atoms.cell}")
print(f"pbc      : {atoms.pbc}")

# "Atomic numbers" and "Mass" can be automatically calculated from "Symbol"
print(f"numbers  : {atoms.numbers}")
print(f"massess  : {atoms.get_masses()}")
print(f"momenta  : {atoms.get_momenta()}")
print(f"Numbers of atoms  : {len(atoms)}")

symbols  : H2
positions: [[0. 0. 0.]
 [1. 0. 0.]]
cell     : Cell([0.0, 0.0, 0.0])
pbc      : [False False False]
numbers  : [1 1]
massess  : [1.008 1.008]
momenta  : [[0. 0. 0.]
 [0. 0. 0.]]
Numbers of atoms  : 2

System of units

In ASE, energy units are often treated in eV (approximately \(1.602 \times 10^{-19}\) J) and coordinate systems in Å (\(1 \times 10^{-10}\) m). The units for force and stress are these composite units: eV/Å for force and eV/Å2 for stress. The unit for charge is the elementary amount of charge.

• eV: Electronvolt

• Å: Angstrom

• e: Elementary charge

[Tips] Detailed information about each class/method can be displayed by appending ? within Jupyter.

Atoms?

Init signature:
Atoms(
    symbols=None,
    positions=None,
    numbers=None,
    tags=None,
    momenta=None,
    masses=None,
    magmoms=None,
    charges=None,
    scaled_positions=None,
    cell=None,
    pbc=None,
    celldisp=None,
    constraint=None,
    calculator=None,
    info=None,
    velocities=None,
)
Docstring:
Atoms object.

The Atoms object can represent an isolated molecule, or a
periodically repeated structure.  It has a unit cell and
there may be periodic boundary conditions along any of the three
unit cell axes.
Information about the atoms (atomic numbers and position) is
stored in ndarrays.  Optionally, there can be information about
tags, momenta, masses, magnetic moments and charges.

In order to calculate energies, forces and stresses, a calculator
object has to attached to the atoms object.

Parameters:

symbols: str (formula) or list of str
    Can be a string formula, a list of symbols or a list of
    Atom objects.  Examples: 'H2O', 'COPt12', ['H', 'H', 'O'],
    [Atom('Ne', (x, y, z)), ...].
positions: list of xyz-positions
    Atomic positions.  Anything that can be converted to an
    ndarray of shape (n, 3) will do: [(x1,y1,z1), (x2,y2,z2),
    ...].
scaled_positions: list of scaled-positions
    Like positions, but given in units of the unit cell.
    Can not be set at the same time as positions.
numbers: list of int
    Atomic numbers (use only one of symbols/numbers).
tags: list of int
    Special purpose tags.
momenta: list of xyz-momenta
    Momenta for all atoms.
masses: list of float
    Atomic masses in atomic units.
magmoms: list of float or list of xyz-values
    Magnetic moments.  Can be either a single value for each atom
    for collinear calculations or three numbers for each atom for
    non-collinear calculations.
charges: list of float
    Initial atomic charges.
cell: 3x3 matrix or length 3 or 6 vector
    Unit cell vectors.  Can also be given as just three
    numbers for orthorhombic cells, or 6 numbers, where
    first three are lengths of unit cell vectors, and the
    other three are angles between them (in degrees), in following order:
    [len(a), len(b), len(c), angle(b,c), angle(a,c), angle(a,b)].
    First vector will lie in x-direction, second in xy-plane,
    and the third one in z-positive subspace.
    Default value: [0, 0, 0].
celldisp: Vector
    Unit cell displacement vector. To visualize a displaced cell
    around the center of mass of a Systems of atoms. Default value
    = (0,0,0)
pbc: one or three bool
    Periodic boundary conditions flags.  Examples: True,
    False, 0, 1, (1, 1, 0), (True, False, False).  Default
    value: False.
constraint: constraint object(s)
    Used for applying one or more constraints during structure
    optimization.
calculator: calculator object
    Used to attach a calculator for calculating energies and atomic
    forces.
info: dict of key-value pairs
    Dictionary of key-value pairs with additional information
    about the system.  The following keys may be used by ase:

      - spacegroup: Spacegroup instance
      - unit_cell: 'conventional' | 'primitive' | int | 3 ints
      - adsorbate_info: Information about special adsorption sites

    Items in the info attribute survives copy and slicing and can
    be stored in and retrieved from trajectory files given that the
    key is a string, the value is JSON-compatible and, if the value is a
    user-defined object, its base class is importable.  One should
    not make any assumptions about the existence of keys.

Examples:

These three are equivalent:

>>> from ase import Atom

>>> d = 1.104  # N2 bondlength
>>> a = Atoms('N2', [(0, 0, 0), (0, 0, d)])
>>> a = Atoms(numbers=[7, 7], positions=[(0, 0, 0), (0, 0, d)])
>>> a = Atoms([Atom('N', (0, 0, 0)), Atom('N', (0, 0, d))])

FCC gold:

>>> a = 4.05  # Gold lattice constant
>>> b = a / 2
>>> fcc = Atoms('Au',
...             cell=[(0, b, b), (b, 0, b), (b, b, 0)],
...             pbc=True)

Hydrogen wire:

>>> d = 0.9  # H-H distance
>>> h = Atoms('H', positions=[(0, 0, 0)],
...           cell=(d, 0, 0),
...           pbc=(1, 0, 0))
File:           ~/.py39/lib/python3.9/site-packages/ase/atoms.py
Type:           type
Subclasses:     Cluster, MSONAtoms, Lattice