Molecular Dynamics simulation¶
TL;DR¶
MD simulations follow the equations of motion of classical mechanics, and the time evolution of the positions and velocities of all atoms can be observed.
The upper limit is generally a few dozen ns due to the time scale limitation. If a phenomenon does not occur within that time, it is necessary to consider a different calculation method.
In MD simulations, there are various states (ensembles) depending on the state to be reproduced, and the simplest ensemble is called the NVE ensemble.
In the NVE ensemble, the total energy conservation law holds, and the time step must be set appropriately in terms of calculation accuracy and calculation time.
In this chapter, you will learn about Molecular dynamics (MD), which simulates the time evolution of a system.
MD simulation explicitly deals with the time evolution of the trajectories of individual atoms. It is a method that calculates the coordinates and velocities of the target atoms sequentially by integrating the equations of motion of classical mechanics. This calculation method itself is a theory independent of models of forces and energies acting between atoms, and has long been used in the field of molecular simulation. Therefore, for the theoretical background and examples, please refer to the existing books and references (for example, [1-3]). The purpose of this tutorial is to acquire the pracitical knowledge necessary to perform these calculations using Matlantis.
Let’s take a look at what can be observed in an MD simulation by running an example.
Preliminary setup - Installation of required libraries¶
Through this chapter, we sometimes use ASAP3-EMT, which is a classical force field easily accessible on ASE. Since it is a classical force field, its accuracy and application are limited, but it is so simple and fast that very useful to demonstrate important points in this tutorial without much hustle and frustration. The elements available in ASAP3-EMT are limited to Ni, Cu, Pd, Ag, Pt, Au and their alloys. The installation procedure is as follows.
[1]:
!pip install --upgrade asap3
Looking in indexes: https://pypi.org/simple, http://pypi.artifact.svc:8080/simple
Collecting asap3
Downloading asap3-3.13.7.tar.gz (855 kB)
━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━ 855.8/855.8 kB 65.4 MB/s eta 0:00:00
Installing build dependencies ... one
Getting requirements to build wheel ... done
Installing backend dependencies ... one
Preparing metadata (pyproject.toml) ... done
Requirement already satisfied: ase>=3.23.0 in /home/jovyan/.py311/lib/python3.11/site-packages (from asap3) (3.25.0)
Requirement already satisfied: numpy>=1.19.5 in /home/jovyan/.py311/lib/python3.11/site-packages (from ase>=3.23.0->asap3) (1.26.4)
Requirement already satisfied: scipy>=1.6.0 in /home/jovyan/.py311/lib/python3.11/site-packages (from ase>=3.23.0->asap3) (1.15.3)
Requirement already satisfied: matplotlib>=3.3.4 in /home/jovyan/.py311/lib/python3.11/site-packages (from ase>=3.23.0->asap3) (3.10.3)
Requirement already satisfied: contourpy>=1.0.1 in /home/jovyan/.py311/lib/python3.11/site-packages (from matplotlib>=3.3.4->ase>=3.23.0->asap3) (1.3.2)
Requirement already satisfied: cycler>=0.10 in /home/jovyan/.py311/lib/python3.11/site-packages (from matplotlib>=3.3.4->ase>=3.23.0->asap3) (0.12.1)
Requirement already satisfied: fonttools>=4.22.0 in /home/jovyan/.py311/lib/python3.11/site-packages (from matplotlib>=3.3.4->ase>=3.23.0->asap3) (4.58.2)
Requirement already satisfied: kiwisolver>=1.3.1 in /home/jovyan/.py311/lib/python3.11/site-packages (from matplotlib>=3.3.4->ase>=3.23.0->asap3) (1.4.8)
Requirement already satisfied: packaging>=20.0 in /home/jovyan/.py311/lib/python3.11/site-packages (from matplotlib>=3.3.4->ase>=3.23.0->asap3) (25.0)
Requirement already satisfied: pillow>=8 in /home/jovyan/.py311/lib/python3.11/site-packages (from matplotlib>=3.3.4->ase>=3.23.0->asap3) (11.2.1)
Requirement already satisfied: pyparsing>=2.3.1 in /home/jovyan/.py311/lib/python3.11/site-packages (from matplotlib>=3.3.4->ase>=3.23.0->asap3) (3.2.3)
Requirement already satisfied: python-dateutil>=2.7 in /home/jovyan/.py311/lib/python3.11/site-packages (from matplotlib>=3.3.4->ase>=3.23.0->asap3) (2.9.0.post0)
Requirement already satisfied: six>=1.5 in /home/jovyan/.py311/lib/python3.11/site-packages (from python-dateutil>=2.7->matplotlib>=3.3.4->ase>=3.23.0->asap3) (1.17.0)
Building wheels for collected packages: asap3
done
Created wheel for asap3: filename=asap3-3.13.7-cp311-cp311-linux_x86_64.whl size=4461488 sha256=8ef68bdc4c47a62e592d5d40598d3921480daf8f34de9a6d3b63d718ff1ec1b7
Stored in directory: /home/jovyan/.cache/pip/wheels/d1/8c/80/5aa8169f1b9773bb685620a4ce577adcd238f95b106ce06013
Successfully built asap3
Installing collected packages: asap3
Successfully installed asap3-3.13.7
[notice] A new release of pip is available: 24.0 -> 25.1.1
[notice] To update, run: pip install --upgrade pip
For details about ASAP3-EMT, please refer ASAP official page.
What can MD simulation do?¶
In the following example, the MD simulation reproduces the molten state of a metallic Al structure. As everyone knows, aluminum is one of the most common metal in both commertial and industrial sectors. Its properties are well known. It has a melting point of 660.3 °C (933.45 K) and the face-centered cubic (fcc) phase is stable over a wide temperature range under ambient pressure. The following shows the process of melting the fcc-Al structure by heating it to an initial temperature of 1600 K. The calculation time is 100 psec.
Fig6-1a. Melting of fcc-Al in NVE ensemble starting at 1600 K
(File: ../input/ch6/6-1_fcc-Al_NVE_1600Kstart.traj)
The Al atoms are initially arranged in a clean fcc crystal structure, but the structure is gradually disrupted and the atoms gradually diffuse out of the simulation cell as the calculation proceeds. In this way, MD simulations allow us to observe in detail the actual trajectories of the atoms as they evolve over time.
Simulation of aluminum melting¶
Below is a sample code of the MD simulation used to reproduce the melting process of fcc-Al described above. The ASAP3 EMT force field is used to speed up the calculation. (To use this force field in your python environment, you must first install the asap3 package by running pip install asap3.) The following calculation runs for 100 psec MD and takes only a few tens of seconds to complete.
[2]:
%%time
import os
from asap3 import EMT
calculator = EMT()
from ase.build import bulk
from ase.md.velocitydistribution import MaxwellBoltzmannDistribution,Stationary
from ase.md.verlet import VelocityVerlet
from ase.md import MDLogger
from ase import units
from time import perf_counter
import numpy as np
# Set up a fcc-Al crystal
atoms = bulk("Al","fcc",a=4.3,cubic=True)
atoms.pbc = True
atoms *= 3
print("atoms = ",atoms)
# Set calculator (EMT in this case)
atoms.calc = calculator
# input parameters
time_step = 1.0 # MD step size in fsec
temperature = 1600 # Temperature in Kelvin
num_md_steps = 100000 # Total number of MD steps
num_interval = 1000 # Print out interval for .log and .traj
# Set the momenta corresponding to the given "temperature"
MaxwellBoltzmannDistribution(atoms, temperature_K=temperature,force_temp=True)
Stationary(atoms) # Set zero total momentum to avoid drifting
# Set output filenames
output_filename = "./output/ch6/liquid-Al_NVE_1.0fs_test"
log_filename = output_filename + ".log"
print("log_filename = ",log_filename)
traj_filename = output_filename + ".traj"
print("traj_filename = ",traj_filename)
# Remove old files if they exist
if os.path.exists(log_filename): os.remove(log_filename)
if os.path.exists(traj_filename): os.remove(traj_filename)
# Define the MD dynamics class object
dyn = VelocityVerlet(atoms,
time_step * units.fs,
trajectory = traj_filename,
loginterval=num_interval
)
# Print statements
def print_dyn():
imd = dyn.get_number_of_steps()
time_md = time_step*imd
etot = atoms.get_total_energy()
ekin = atoms.get_kinetic_energy()
epot = atoms.get_potential_energy()
temp_K = atoms.get_temperature()
print(f" {imd: >3} {etot:.9f} {ekin:.9f} {epot:.9f} {temp_K:.2f}")
dyn.attach(print_dyn, interval=num_interval)
# Set MD logger
dyn.attach(MDLogger(dyn, atoms, log_filename, header=True, stress=False,peratom=False, mode="w"), interval=num_interval)
# Now run MD simulation
print(f"\n imd Etot(eV) Ekin(eV) Epot(eV) T(K)")
dyn.run(num_md_steps)
print("\nNormal termination of the MD run!")
atoms = Atoms(symbols='Al108', pbc=True, cell=[12.899999999999999, 12.899999999999999, 12.899999999999999])
log_filename = ./output/ch6/liquid-Al_NVE_1.0fs_test.log
traj_filename = ./output/ch6/liquid-Al_NVE_1.0fs_test.traj
imd Etot(eV) Ekin(eV) Epot(eV) T(K)
0 32.139701294 22.336120234 9.803581060 1600.00
1000 32.144722159 9.393665122 22.751057037 672.90
2000 32.144501700 10.379779872 21.764721828 743.53
3000 32.144318649 10.246193775 21.898124875 733.96
4000 32.144092145 11.057828314 21.086263831 792.10
5000 32.144046250 11.951114265 20.192931985 856.09
6000 32.144260378 10.923214025 21.221046353 782.46
7000 32.144403860 10.881528388 21.262875472 779.47
8000 32.144603170 10.966654516 21.177948654 785.57
9000 32.144375218 11.119079419 21.025295799 796.49
10000 32.144222322 11.189498687 20.954723635 801.54
11000 32.144440573 9.685355360 22.459085213 693.79
12000 32.144344847 10.762266046 21.382078801 770.93
13000 32.144479122 8.902966113 23.241513009 637.74
14000 32.144045468 11.006792340 21.137253128 788.45
15000 32.144403754 10.902851629 21.241552125 781.00
16000 32.144707168 9.021035461 23.123671707 646.20
17000 32.144642186 10.023978285 22.120663901 718.05
18000 32.144529839 10.291094693 21.853435146 737.18
19000 32.144050744 11.312184244 20.831866500 810.32
20000 32.144890930 9.067681632 23.077209298 649.54
21000 32.143962314 11.384761628 20.759200686 815.52
22000 32.144291661 11.076124249 21.068167412 793.41
23000 32.144432732 10.505241125 21.639191607 752.52
24000 32.144434143 9.677110695 22.467323448 693.20
25000 32.144411792 10.096105345 22.048306447 723.21
26000 32.144418684 10.314244415 21.830174269 738.84
27000 32.144056137 10.819549400 21.324506737 775.04
28000 32.144136380 10.282863144 21.861273236 736.59
29000 32.144064247 10.603706988 21.540357259 759.57
30000 32.144142785 10.559098906 21.585043879 756.38
31000 32.144361966 9.657395222 22.486966744 691.79
32000 32.144754870 8.707546903 23.437207967 623.75
33000 32.144403555 10.326549807 21.817853748 739.72
34000 32.143748162 11.951159073 20.192589088 856.10
35000 32.144315603 10.100633141 22.043682462 723.54
36000 32.144494671 9.299422264 22.845072408 666.14
37000 32.144459312 10.264518196 21.879941116 735.28
38000 32.144381071 10.328971396 21.815409675 739.89
39000 32.143938348 10.560093761 21.583844587 756.45
40000 32.144102210 10.942980034 21.201122176 783.88
41000 32.144304063 9.758359111 22.385944952 699.02
42000 32.144112774 10.411570083 21.732542691 745.81
43000 32.144261663 11.015808525 21.128453137 789.09
44000 32.143624324 11.206493107 20.937131217 802.75
45000 32.143866741 10.944182507 21.199684234 783.96
46000 32.144367770 9.874633405 22.269734364 707.35
47000 32.143616353 11.287305027 20.856311326 808.54
48000 32.144377245 10.154501900 21.989875345 727.40
49000 32.144159709 10.059211532 22.084948176 720.57
50000 32.144028665 9.486133089 22.657895576 679.52
51000 32.143870407 10.461223944 21.682646463 749.37
52000 32.144010351 11.677881834 20.466128517 836.52
53000 32.143902994 11.086181772 21.057721222 794.13
54000 32.144209243 10.877133213 21.267076030 779.16
55000 32.143866159 11.672773150 20.471093009 836.15
56000 32.144245550 10.188169764 21.956075786 729.81
57000 32.144065429 10.540759442 21.603305987 755.06
58000 32.144047181 11.236293826 20.907753356 804.89
59000 32.144231273 10.845868548 21.298362725 776.92
60000 32.144175394 10.095420061 22.048755333 723.16
61000 32.144210124 10.751451533 21.392758591 770.16
62000 32.144358234 9.409524372 22.734833861 674.03
63000 32.144063044 10.947444309 21.196618735 784.20
64000 32.144231053 11.017702487 21.126528566 789.23
65000 32.144695236 9.546443148 22.598252088 683.84
66000 32.144162224 11.276822936 20.867339288 807.79
67000 32.144488062 10.519866599 21.624621463 753.57
68000 32.144557555 10.129716371 22.014841184 725.62
69000 32.144450322 10.284807689 21.859642633 736.73
70000 32.144447181 10.400649435 21.743797746 745.03
71000 32.144632289 9.627578409 22.517053880 689.65
72000 32.144341422 10.961964783 21.182376639 785.24
73000 32.144545573 10.711859413 21.432686160 767.32
74000 32.144810591 9.861638540 22.283172051 706.42
75000 32.144743025 10.142373359 22.002369665 726.53
76000 32.144666166 10.330929323 21.813736843 740.03
77000 32.145018460 9.962101343 22.182917118 713.61
78000 32.144948334 10.163190408 21.981757925 728.02
79000 32.144724224 10.841427576 21.303296648 776.60
80000 32.144567401 10.946160891 21.198406510 784.10
81000 32.144693558 10.170510668 21.974182891 728.54
82000 32.144802089 9.862497743 22.282304346 706.48
83000 32.145176925 9.213573320 22.931603605 659.99
84000 32.145220296 9.216727852 22.928492444 660.22
85000 32.145225359 8.782294025 23.362931334 629.10
86000 32.145009261 7.957304052 24.187705209 570.00
87000 32.144947628 8.411435060 23.733512568 602.54
88000 32.144898967 8.540565949 23.604333018 611.79
89000 32.145000371 8.278721461 23.866278910 593.03
90000 32.144782624 8.383947198 23.760835427 600.57
91000 32.145227363 8.091000385 24.054226978 579.58
92000 32.144911313 8.987582334 23.157328979 643.81
93000 32.145250110 7.310771383 24.834478726 523.69
94000 32.144846879 9.663598769 22.481248111 692.23
95000 32.145210301 8.115149170 24.030061131 581.31
96000 32.144906799 8.290101213 23.854805586 593.84
97000 32.144800583 7.827986525 24.316814058 560.74
98000 32.145024360 8.451294407 23.693729953 605.39
99000 32.144819857 8.631967805 23.512852051 618.33
100000 32.145028766 8.010498131 24.134530635 573.81
Normal termination of the MD run!
CPU times: user 25.6 s, sys: 203 ms, total: 25.8 s
Wall time: 25.6 s
The flow of the program can be understood by looking at the comments in the script, but the important points are explained here.
(1) Initial velocity distribution
Once the structure has been created and the calculation parameters have been set, the initial velocity of each atom is given by a velocity distribution corresponding to the specified temperature Maxwell-Boltzmann distribution. This is done using the MaxwellBoltzmannDistribution in above code. Since the initial velocity given by this method has arbitrary momentum of the whole system, there is a possibility that the
whole system may drift. Therefore, after giving the initial velocity by MaxwellBoltzmannDistribution, we set the momentum of the entire system to zero by the Stationary method and fix the coordinates of the center of mass. This is important not only for the NVE case, but also for simulations involving temperature and pressure control that will follow.
(2) Execute MD
This time, MD by Verlet integration is executed using the class VelocityVerlet. MD is actually executed at dyn.run(num_md_steps). In this time, time_step=1.0 (time width of 1fs = \(1 \times 10^{-15}\) sec per step) is used to execute num_md_steps=100000 steps.
(3) Recording of calculation results
The script has a method named print_dyn that prints energy and temperature values to standard output (output on a notebook). There is another class, MDLogger, which outputs energy, temperature, and stress information in a specified log file. You can define your own class to output the calculation results to a file, but the default logger provides the necessary information for most applications, so it is recommended to utilize it.
After MD is executed, the trajectory can be visualized as follows.
[3]:
from ase.io import Trajectory
from pfcc_extras.visualize.view import view_ngl
traj = Trajectory(traj_filename)
view_ngl(traj)
[3]:
[4]:
from pfcc_extras.visualize.povray import traj_to_apng
from IPython.display import Image
traj_to_apng(traj, f"output/Fig6-1_fcc-Al_NVE_1600Kstart.png", rotation="0x,0y,0z", clean=True, n_jobs=16)
# See Fig6-1a
#Image(url="output/Fig6-1_fcc-Al_NVE_1600Kstart.png")
[Parallel(n_jobs=16)]: Using backend ThreadingBackend with 16 concurrent workers.
[Parallel(n_jobs=16)]: Done 18 tasks | elapsed: 12.8s
[Parallel(n_jobs=16)]: Done 101 out of 101 | elapsed: 41.7s finished
History of physical properties in NVE ensembles¶
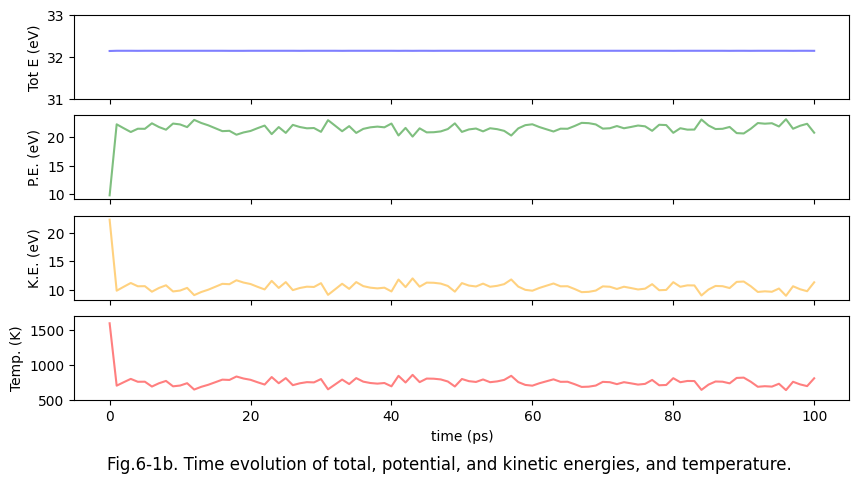
Since the velocity (i.e., momentum) of each atom is known, the history of the various energies of the system can be followed. For example, here are the time profiles of total energy (Tot.E.), potential energy (P.E.), kinetic energy (K.E.), and temperature (Temp.) for the melting of fcc-Al.
[5]:
import pandas as pd
df = pd.read_csv(log_filename, delim_whitespace=True)
df
/tmp/ipykernel_50921/510401485.py:3: FutureWarning: The 'delim_whitespace' keyword in pd.read_csv is deprecated and will be removed in a future version. Use ``sep='\s+'`` instead
df = pd.read_csv(log_filename, delim_whitespace=True)
[5]:
| Time[ps] | Etot[eV] | Epot[eV] | Ekin[eV] | T[K] | |
|---|---|---|---|---|---|
| 0 | 0.0 | 32.140 | 9.804 | 22.336 | 1600.0 |
| 1 | 1.0 | 32.145 | 22.751 | 9.394 | 672.9 |
| 2 | 2.0 | 32.145 | 21.765 | 10.380 | 743.5 |
| 3 | 3.0 | 32.144 | 21.898 | 10.246 | 734.0 |
| 4 | 4.0 | 32.144 | 21.086 | 11.058 | 792.1 |
| ... | ... | ... | ... | ... | ... |
| 96 | 96.0 | 32.145 | 23.855 | 8.290 | 593.8 |
| 97 | 97.0 | 32.145 | 24.317 | 7.828 | 560.7 |
| 98 | 98.0 | 32.145 | 23.694 | 8.451 | 605.4 |
| 99 | 99.0 | 32.145 | 23.513 | 8.632 | 618.3 |
| 100 | 100.0 | 32.145 | 24.135 | 8.010 | 573.8 |
101 rows × 5 columns
[6]:
import numpy as np
import matplotlib.pyplot as plt
fig = plt.figure(figsize=(10, 5))
#color = 'tab:grey'
ax1 = fig.add_subplot(4, 1, 1)
ax1.set_xticklabels([])
ax1.set_ylabel('Tot E (eV)')
ax1.set_ylim([31.,33.])
ax1.plot(df["Time[ps]"], df["Etot[eV]"], color="blue",alpha=0.5)
ax2 = fig.add_subplot(4, 1, 2)
ax2.set_xticklabels([])
ax2.set_ylabel('P.E. (eV)')
ax2.plot(df["Time[ps]"], df["Epot[eV]"], color="green",alpha=0.5)
ax3 = fig.add_subplot(4, 1, 3)
ax3.set_xticklabels([])
ax3.set_ylabel('K.E. (eV)')
ax3.plot(df["Time[ps]"], df["Ekin[eV]"], color="orange",alpha=0.5)
ax4 = fig.add_subplot(4, 1, 4)
ax4.set_xlabel('time (ps)')
ax4.set_ylabel('Temp. (K)')
ax4.plot(df["Time[ps]"], df["T[K]"], color="red",alpha=0.5)
ax4.set_ylim([500., 1700])
fig.suptitle("Fig.6-1b. Time evolution of total, potential, and kinetic energies, and temperature.", y=0)
#plt.savefig("6-1_liquid-Al_NVE_1.0fs_test_E_vs_t.png") # <- Use if saving to an image file is desired
plt.show()
As mentioned in section 1-5, the total energy \(E\) of a system is expressed by the kinetic energy \(K\) and the potential energy \(V\).
Of these, the kinetic energy \(K\) of a system can be calculated as follows, using the formula from classical mechanics.
where \(m_i, \mathbf{v}_i, \mathbf{p}_i\) are the mass, velocity and momentum (\(\mathbf{p}=m\mathbf{v}\)) of each atom respectively. Here, the temperature and kinetic energy of the system are synonymous and are defined by the following relationship.
In this case, the initial temperature is set to 1600 K, and the system evolves naturally in time according to the equations of motion of classical mechanics. Since there is no external force, the energy conservation law is obeyed and the total energy is kept constant within the numerical error. The temperature decreases fairly quickly, and the kinetic and potential energies follows the equipartition theorem, and the temperature eventually settles to about half the initial temperature. This is how matter actually behaves in nature, and the simplest MD simulations such as this one reproduce such a situation. The distribution of states of such a system is shown in NVE Ensemble. (or microcanonical ensemble, where N stands for the number of atoms, V for the volume, and E for the total energy being constant.) The ensemble here refers to the distribution of states of system in the concept of statistical mechanics.
MD simulation parameters in NVE ensemble¶
In the MD simulation of the NVE ensemble described above, you need to set the calculation conditions like initial temperature and calculation time. In addition, we also need to set the MD time step as a relatively non-trivial parameter. How should this MD time step be set?
The answer depends on the accuracy of the calculation you are looking for: the NVE ensemble solves the classical equations of motion, which are second-order ordinary differential equations, and the accuracy of this integration process is determined by the size of the time step. (more details on integration methods are given at the end of this section). Let us see how the total energy changes when the time step is changed. Let us assume that the computation time is 1 nsec. (This is a time scale often used in classical MD.)
Fig.6-1c. Time evolution of the total energy with respect to time step size.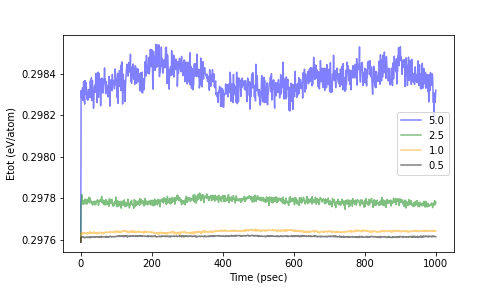
The above figure shows the calculation results when the time step is varied from 0.5 to 5.0 fsec. It can be seen that the total energy, which should be constant, has a large deviation with time evolution when the time step is large.
To check the time dependence of the total energy, run the above MD simulation script with different time_step arguments and compare the energy profiles as an excercise. For visualization, please refer to the visualization code shown in Fig. 6-1b above.
Varying the MD time step from the above calculations and plotting the RMSE obtained from the total energy fluctuations on the horizontal axis for the time step and the vertical axis for the total energy fluctuations, the results are shown below.
Fig.6-1d. Total energy ERMSE as a function of MD step size.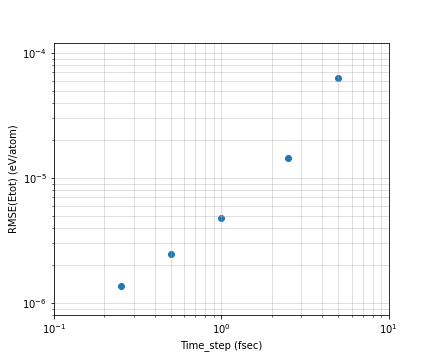
The vertical axis is the energy per atom, the plots can be seen to be roughly linear in a log-log plot. The energy per atom varies from 1.2e-6 eV at 0.25 fs to 6e-5 fs at 5.0 fs. In this case, the number of atoms is 108, so we can confirm that the entire system can vary from 1e-4 eV to 1e-3 eV.
In terms of energy, assuming a time step of 1 fsec, an error of about 0.5 meV is expected for a 100 atom system for a 1 nsec simulation, and about 5 meV for a 1000 atom system. Of course, it depends on the physical properties you want to calculate, but for most calculations, this should be accurate enough. If the time step is set to 5 fsec to increase the calculation time, the error will increase by about one order of magnitude. When using MD calculations, it is necessary to keep in mind the degree of accuracy of these calculations.
Other ensembles and MD Simulations¶
At the end of this section, we will discuss MD simulation methods other than NVE ensembles.
MD simulations of NVE ensembles are simple and powerful, but they have many disadvantages when it comes to reproducing the phenomena we generally want to observe. The atoms in the cell is all the computation target in the NVE simulation, and there is no external world. However, the microscopic world we actually want to observe has an environment surrounding it. The temperature and pressure of the external environment will change the state of the system of interest, which cannot be reproduced within the scope of the NVE ensemble.
There are various state distributions such as canonical ensemble (NVT), isothermal-isobaric ensemble (NPT), etc. in statistical mechanics, and they can be utilized to perform calculations under specific conditions. In the following sections, you will learn how to perform calculations under these statistical ensembles.
Reference¶
[1] M.P. Allen and D.J. Tildesley, “Computer simulaiton of liquid”, 2nd Ed., Oxford University Press (2017) ISBN 978-0-19-880319-5. DOI:10.1093/oso/9780198803195.001.0001
[2] D. Frenkel and B. Smit “Understanding molecular simulation - from algorithms to applications”, 2nd Ed., Academic Press (2002) ISBN 978-0-12-267351-1. DOI:10.1016/B978-0-12-267351-1.X5000-7
[3] M.E. Tuckerman, “Statistical mechanics: Theory and molecular simulation”, Oxford University Press (2010) ISBN 978-0-19-852526-4. https://global.oup.com/academic/product/statistical-mechanics-9780198525264?q=Statistical%20mechanics:%20Theory%20and%20molecular%20simulation&cc=gb&lang=en#