NPT ensemble¶
TL;DR¶
In NPT-MD simulations, pressure and temperature are controlled and remain constant once the system reaches equilibrium. There are two common pressure control (barostat) methods available in ASE: the Parrinello-Rahman method and the Berendsen method.
Typical applications include simulations of thermal expansion, phase transitions, and pressurization of solids and fluids.
In the Parrinello-Rahman method, all degrees of freedom of the simulation cell are variable, and the control parameter (
pfactor) must be set appropriately.Berendsen barostat, like Berendsen thermostat, can control pressure efficiently for convergence; Berendsen barostat can be calculated in two modes: with fixed cell angles and independently variable cell lengths, or with fixed cell length ratios.
compressibilitymust be properly set as an input parameter.
In this section, we will discuss a method to create an equilibrium state in which both pressure and temperature are constant. The pressure control mechanism is generally referred to as barostat, and is used in conjunction with the thermostat method described in section 6-2 to generate a state distribution called an isothermal-isobaric ensemble (also known as NPT).
Phenomena that can be studied, in principle, in NPT-MD simulations include
Coefficient of thermal expansion of solids
Prediction of melting point
Phase transitions in solids
Density prediction of fluids (gases and liquids)
etc.
The reason why the word “in principle” is used is that the reproducibility of these phenomena depends greatly on the accuracy of the force field used in the calculation, and in particular, it is known to be very difficult to predict intermolecular forces and fluid states that depend on small energy differences. In this tutorial, we will learn about NPT-MD through the case study of solids, which are considered to have relatively high accuracy.
First, we will review the NPT-MD methods implemented in ASE that we will use in this tutorial. There are three types of implementations available for ASE
Class |
Ensemble |
Parameter |
thermostat |
barostat |
description |
|---|---|---|---|---|---|
NPT |
NPT |
time constant (\(\tau_t\)), pressure factor (pfactor) |
Nosé–Hoover |
Parrinello-Rahman |
セルの全All degrees of freedom of the cell are variable and controllable |
NPTBerendsen |
NPT |
\(\tau_t\),\(\tau_P\),\(\beta_T\) |
Berendsen |
Berendsen |
Cell shape is maintained and only volume changes |
InhomogeneousBerendsen |
NPT |
\(\tau_t\),\(\tau_P\),\(\beta_T\) |
Berendsen |
Berendsen |
Cell angles are preserved, but pressure anisotropy can be taken into account |
The second and third methods in the table are essentially the same Berendsen barostat. (The third method, InhomogeneousBerendsen, is not mentioned in the ASE manual, but is defined as a class within ASE along with NPTBerendsen.) Thus, there are only two methods available within the ASE framework: the Parrinello-Rahman method and the Berendsen method. The heat bath itself uses the methods described in section 6-2, so the characteristics of these heat bath methods should be carefully
considered.
Let us first look at the Parrinello-Rahman method, which has relatively high system flexibility and versatility.
Equations of motion for the Parrinello-Rahman method¶
The Parrinello-Rahman method is a so-called extended system calculation method, which assumes that the system under consideration is hypothetically connected to an external system of constant temperature and pressure, as in the Nosé-Hoover heat bath method. In this case, the equations of motion are written as follows (For details of the derivation, please refer to references [1-3]).
Besides the terms for the Nosé-Hoover heat bath, we have the pressure control time constant \(\tau_P\), the system center of mass \(R_o\), the target external pressure \(P_o\), and the simulation cell volume \(V\). The \(\eta\) is the variable for the pressure control degrees of freedom. \(\mathbf{h} = (\mathbf{a}, \mathbf{b}, \mathbf{c})\) and \(\mathbf{a},\mathbf{b},\mathbf{c}\) are cell vectors defining each edge of the simulation cell, respectively.
In addition to temperature \(T_o\) and pressure \(P_o\), there are two other values that the user must set in the above equation: \(\tau_T\) and \(\tau_P\). First, the case where \(\tau_T\) and \(\tau_P\) are simply set to random values is shown below. Here \(\tau_T\) is set to 20 fsec. Although \(\tau_P\) is not specified directly, the value called pfactor is \(\tau_P^2B\). The \(B\) refers to the bulk modulus, and this value must be calculated and
specified in advance. However, since the exact value of \(\tau_P\) itself is not known in advance, there is no way to specify pfactor. Also, the value of \(B\) cannot be calculated for anisotropic structures or when different types of materials coexist in the system. Therefore, we will set an approximate value of pfactor to examine the behavior of the barostat. As mentioned in the following example, at least for crystalline metal systems, a value on the order of about
10\(^6\) GPa\(\cdot\)fs\(^2\) to 10\(^7\) GPa\(\cdot\)fs\(^2\) seems to give good convergence and stability in the calculation. For other materials, it is recommended to play with the value of pfactor and check the behavior of the volume change as a preliminary study.
Calculation example: Coefficient of thermal expansion¶
Now, we will use the Nosé-Hoover thermostat and the Parrinello-Rahman barostat (ASE’s NPT class) to compute the coefficient of thermal expansion of a solid as an example. The system is equilibrated at temperatures of given increment, and the thermal expansion coefficient is calculated from the average value of the lattice constant at each temperature.
For simplicity, we will use fcc-Cu for this calculation. A sample script is shown below. The temperature is varied from 200 K to 1000 K in 100 K interval and the external pressure is set to 1 bar. The structure is fcc-Cu extended to 3x3x3 unit cells with 108 atoms. In the example, the ASAP3-EMT force field is used for speed, but the same scheme can be used with PFP. The time step size is set to 1 fs, and the 20 ps simulation is found to be sufficient to reach equilibrium.
[1]:
import ase
from ase.build import bulk
from ase.md.velocitydistribution import MaxwellBoltzmannDistribution,Stationary
from ase.md.npt import NPT
from ase.md import MDLogger
from ase import units
from time import perf_counter
calc_type = "EMT"
# calc_type = "PFP"
if calc_type == "EMT":
# ASAP3-EMT calculator
from asap3 import EMT
calculator = EMT()
elif calc_type == "PFP":
# PFP calculator
from pfp_api_client.pfp.estimator import Estimator, EstimatorCalcMode
from pfp_api_client.pfp.calculators.ase_calculator import ASECalculator
estimator = Estimator(calc_mode=EstimatorCalcMode.PBE, model_version="v8.0.0")
calculator = ASECalculator(estimator)
else:
raise ValueError(f"Wrong calc_type = {calc_type}!")
# Set up a crystal
atoms_in = bulk("Cu",cubic=True)
atoms_in *= 3
atoms_in.pbc = True
print("atoms_in = ",atoms_in)
# input parameters
time_step = 1.0 # fsec
#temperature = 300 # Kelvin
num_md_steps = 20000
num_interval = 10
sigma = 1.0 # External pressure in bar
ttime = 20.0 # Time constant in fs
pfactor = 2e6 # Barostat parameter in GPa
temperature_list = [200,300,400,500,600,700,800,900,1000]
# Print statements
def print_dyn():
imd = dyn.get_number_of_steps()
etot = atoms.get_total_energy()
temp_K = atoms.get_temperature()
stress = atoms.get_stress(include_ideal_gas=True)/units.GPa
stress_ave = (stress[0]+stress[1]+stress[2])/3.0
elapsed_time = perf_counter() - start_time
print(f" {imd: >3} {etot:.3f} {temp_K:.2f} {stress_ave:.2f} {stress[0]:.2f} {stress[1]:.2f} {stress[2]:.2f} {stress[3]:.2f} {stress[4]:.2f} {stress[5]:.2f} {elapsed_time:.3f}")
# run MD
for i,temperature in enumerate(temperature_list):
print("i,temperature = ",i,temperature)
print(f"sigma = {sigma:.1e} bar")
print(f"ttime = {ttime:.3f} fs")
print(f"pfactor = {pfactor:.3f} GPa*fs^2")
temperature_str = str(int(temperature)).zfill(4)
output_filename = f"./output/ch6/fcc-Cu_3x3x3_NPT_{calc_type}_{temperature_str}K"
log_filename = output_filename + ".log"
traj_filename = output_filename + ".traj"
print("log_filename = ",log_filename)
print("traj_filename = ",traj_filename)
atoms = atoms_in.copy()
atoms.calc = calculator
# Set the momenta corresponding to T=300K
MaxwellBoltzmannDistribution(atoms, temperature_K=temperature,force_temp=True)
Stationary(atoms)
dyn = NPT(atoms,
time_step*units.fs,
temperature_K = temperature,
externalstress = sigma*units.bar,
ttime = ttime*units.fs,
pfactor = pfactor*units.GPa*(units.fs**2),
logfile = log_filename,
trajectory = traj_filename,
loginterval=num_interval
)
print_interval = 1000 if calc_type == "EMT" else num_interval
dyn.attach(print_dyn, interval=print_interval)
dyn.attach(MDLogger(dyn, atoms, log_filename, header=True, stress=True, peratom=True, mode="a"), interval=num_interval)
# Now run the dynamics
start_time = perf_counter()
print(f" imd Etot(eV) T(K) stress(mean,xx,yy,zz,yz,xz,xy)(GPa) elapsed_time(sec)")
dyn.run(num_md_steps)
atoms_in = Atoms(symbols='Cu108', pbc=True, cell=[10.83, 10.83, 10.83])
i,temperature = 0 200
sigma = 1.0e+00 bar
ttime = 20.000 fs
pfactor = 2000000.000 GPa*fs^2
log_filename = ./output/ch6/fcc-Cu_3x3x3_NPT_EMT_0200K.log
traj_filename = ./output/ch6/fcc-Cu_3x3x3_NPT_EMT_0200K.traj
imd Etot(eV) T(K) stress(mean,xx,yy,zz,yz,xz,xy)(GPa) elapsed_time(sec)
0 2.727 200.00 1.64 1.62 1.66 1.63 -0.03 -0.00 0.04 0.004
1000 3.257 138.10 0.86 0.84 0.84 0.88 0.17 0.17 0.21 1.304
2000 4.444 192.41 0.77 0.61 0.92 0.79 0.29 0.27 -0.04 2.563
3000 4.381 187.60 0.93 1.03 0.94 0.84 0.12 0.08 0.30 3.808
4000 4.599 181.45 0.52 0.42 0.76 0.39 0.05 0.05 0.21 5.072
5000 5.692 202.32 -0.38 -0.38 -0.35 -0.41 -0.06 0.56 0.25 6.414
6000 6.109 220.68 -0.65 -0.74 -0.68 -0.52 -0.20 0.02 0.04 7.671
7000 5.639 219.03 -0.15 0.01 -0.36 -0.10 0.04 0.15 -0.01 8.902
8000 5.351 205.21 0.45 0.44 0.39 0.53 0.05 0.24 -0.04 10.165
9000 5.376 174.50 0.22 0.05 0.42 0.18 0.18 0.15 -0.17 11.484
10000 5.744 196.53 -0.33 -0.46 -0.25 -0.27 0.05 -0.02 0.09 12.785
11000 5.523 230.52 -0.30 -0.31 -0.43 -0.17 -0.00 0.05 0.15 14.047
12000 4.885 184.51 -0.11 -0.14 -0.08 -0.13 0.30 0.12 -0.05 15.302
13000 5.545 213.75 0.18 0.34 0.14 0.06 0.55 -0.12 0.03 16.610
14000 6.289 218.35 0.14 0.21 0.33 -0.12 0.33 0.25 0.12 17.857
15000 5.202 205.62 0.44 0.28 0.56 0.48 0.39 -0.08 -0.00 19.133
16000 5.704 211.51 -0.37 -0.55 -0.22 -0.34 0.05 -0.40 -0.18 20.411
17000 5.178 184.93 -0.52 -0.41 -0.71 -0.45 0.04 -0.17 -0.10 21.694
18000 5.410 192.98 -0.25 -0.03 -0.46 -0.27 0.08 -0.11 -0.26 22.949
19000 6.283 234.67 0.13 0.31 -0.06 0.15 -0.06 -0.20 -0.16 24.195
20000 5.147 180.81 0.62 0.69 0.56 0.60 -0.14 -0.20 -0.49 25.469
i,temperature = 1 300
sigma = 1.0e+00 bar
ttime = 20.000 fs
pfactor = 2000000.000 GPa*fs^2
log_filename = ./output/ch6/fcc-Cu_3x3x3_NPT_EMT_0300K.log
traj_filename = ./output/ch6/fcc-Cu_3x3x3_NPT_EMT_0300K.traj
imd Etot(eV) T(K) stress(mean,xx,yy,zz,yz,xz,xy)(GPa) elapsed_time(sec)
0 4.123 300.00 1.52 1.61 1.46 1.50 -0.01 -0.03 -0.01 0.002
1000 7.039 294.54 0.62 0.76 0.50 0.62 -0.02 -0.11 -0.11 1.289
2000 6.642 266.68 1.46 1.74 1.57 1.06 -0.25 0.02 0.05 2.559
3000 7.757 288.57 1.48 1.52 1.57 1.34 -0.15 -0.16 0.39 3.823
4000 8.489 291.95 0.31 0.34 -0.02 0.61 0.08 -0.08 0.58 5.096
5000 8.163 265.87 -0.89 -1.07 -1.04 -0.57 0.11 0.19 0.65 6.381
6000 8.944 336.60 -1.32 -1.24 -1.20 -1.53 0.20 0.60 0.37 7.666
7000 7.524 257.73 -0.28 -0.18 -0.06 -0.62 -0.13 0.11 0.52 8.908
8000 8.845 311.11 0.50 0.57 0.61 0.32 0.21 0.36 0.73 10.169
9000 8.675 306.12 1.05 1.08 0.82 1.24 0.52 0.10 0.73 11.489
10000 8.658 313.89 0.58 0.47 0.39 0.87 0.74 0.14 0.74 12.752
11000 9.631 395.51 -0.49 -0.43 -0.62 -0.41 0.52 0.40 0.70 13.999
12000 8.691 286.93 -1.19 -0.96 -1.09 -1.52 0.28 0.22 0.49 15.278
13000 7.403 260.96 -0.60 -0.56 -0.29 -0.95 0.51 -0.03 0.44 16.553
14000 9.016 325.97 -0.14 -0.04 -0.17 -0.21 0.54 -0.07 0.80 17.834
15000 9.425 316.12 0.55 0.62 0.28 0.76 0.44 0.02 0.89 19.086
16000 8.362 287.70 0.83 0.60 0.85 1.05 0.38 0.08 0.89 20.360
17000 8.799 292.57 -0.21 -0.49 0.24 -0.37 -0.02 -0.38 0.91 21.664
18000 8.024 293.51 -0.65 -0.50 -0.71 -0.73 -0.23 0.08 1.02 22.930
19000 8.160 303.79 -0.84 -0.47 -1.30 -0.73 -0.11 -0.19 1.18 24.190
20000 9.328 351.21 -0.45 -0.40 -0.89 -0.06 -0.17 -0.22 1.09 25.461
i,temperature = 2 400
sigma = 1.0e+00 bar
ttime = 20.000 fs
pfactor = 2000000.000 GPa*fs^2
log_filename = ./output/ch6/fcc-Cu_3x3x3_NPT_EMT_0400K.log
traj_filename = ./output/ch6/fcc-Cu_3x3x3_NPT_EMT_0400K.traj
imd Etot(eV) T(K) stress(mean,xx,yy,zz,yz,xz,xy)(GPa) elapsed_time(sec)
0 5.519 400.00 1.40 1.47 1.33 1.41 -0.07 0.04 -0.06 0.003
1000 11.615 433.05 -1.87 -1.41 -2.02 -2.19 -0.34 -0.03 -0.12 1.265
2000 12.383 419.09 -0.11 0.46 0.03 -0.82 -0.31 -0.01 0.22 2.529
3000 11.877 413.81 2.05 2.38 2.37 1.39 -0.11 0.04 -0.28 3.805
4000 11.944 409.88 2.15 1.89 2.46 2.11 0.18 -0.01 -0.21 5.076
5000 11.040 381.69 0.96 0.81 0.82 1.26 0.10 -0.00 0.60 6.369
6000 10.106 394.10 -0.40 -0.22 -1.01 0.04 -0.02 -0.30 0.23 7.647
7000 10.675 424.80 -1.73 -1.60 -1.97 -1.60 -0.13 -0.82 0.54 8.945
8000 11.052 382.51 -1.81 -1.64 -1.59 -2.21 -0.24 -0.54 -0.04 10.224
9000 11.590 414.92 -0.36 -0.14 -0.16 -0.79 -0.56 -0.64 0.28 11.498
10000 10.523 341.87 1.38 1.67 1.18 1.27 -0.14 -0.24 0.33 12.762
11000 10.769 359.31 1.98 2.01 1.77 2.15 0.27 -0.08 0.19 14.014
12000 11.827 390.91 0.78 0.84 0.67 0.81 0.17 -0.72 0.01 15.283
13000 11.848 448.43 -0.54 -0.82 -0.11 -0.68 0.49 -0.85 0.76 16.570
14000 10.131 371.62 -1.29 -1.31 -0.92 -1.64 -0.22 -0.86 0.65 17.851
15000 10.884 413.01 -1.32 -1.05 -1.42 -1.49 0.33 -0.59 0.60 19.117
16000 10.524 347.84 -0.50 -0.26 -1.03 -0.22 0.27 -1.27 0.16 20.391
17000 12.336 410.07 0.30 0.30 0.49 0.11 0.38 -0.29 0.34 21.652
18000 11.884 372.32 1.41 0.92 2.28 1.03 0.50 -0.44 0.32 22.936
19000 11.505 398.81 1.77 1.47 2.62 1.22 -0.01 -0.95 0.20 24.188
20000 11.140 403.94 0.67 0.88 0.21 0.92 -0.05 -0.59 -0.48 25.481
i,temperature = 3 500
sigma = 1.0e+00 bar
ttime = 20.000 fs
pfactor = 2000000.000 GPa*fs^2
log_filename = ./output/ch6/fcc-Cu_3x3x3_NPT_EMT_0500K.log
traj_filename = ./output/ch6/fcc-Cu_3x3x3_NPT_EMT_0500K.traj
imd Etot(eV) T(K) stress(mean,xx,yy,zz,yz,xz,xy)(GPa) elapsed_time(sec)
0 6.915 500.00 1.29 1.31 1.29 1.27 0.05 -0.06 -0.06 0.003
1000 12.058 479.42 -1.63 -1.76 -1.58 -1.57 -0.08 0.32 0.65 1.308
2000 12.707 510.71 0.12 -0.36 0.33 0.38 -0.04 0.75 -0.04 2.558
3000 15.222 539.00 1.53 1.90 1.36 1.32 -0.24 0.64 0.21 3.825
4000 14.956 487.91 3.19 3.80 2.80 2.96 -0.11 0.89 0.05 5.093
5000 16.151 489.16 3.07 2.97 3.59 2.64 -0.13 0.75 0.43 6.351
6000 15.795 561.85 2.81 2.43 3.07 2.93 -0.09 0.32 0.57 7.608
7000 13.226 489.39 1.42 1.18 1.52 1.56 0.09 0.27 -0.35 8.856
8000 13.933 547.11 -1.62 -1.45 -1.61 -1.79 0.01 0.47 -0.56 10.128
9000 14.159 497.65 -3.89 -3.67 -3.95 -4.06 0.13 0.59 -0.26 11.450
10000 13.296 480.78 -3.69 -3.94 -4.40 -2.74 0.40 0.33 -0.59 12.716
11000 13.504 483.52 -1.88 -2.03 -1.77 -1.84 0.84 0.56 -0.95 13.992
12000 13.670 457.77 0.13 0.35 0.23 -0.19 0.59 0.35 -0.08 15.287
13000 15.112 553.76 1.80 2.25 2.06 1.09 -0.05 0.72 -0.22 16.557
14000 16.743 627.12 2.40 2.63 2.49 2.08 -0.45 0.90 -0.51 17.804
15000 15.498 497.26 1.54 1.58 0.95 2.11 -0.65 0.32 -0.69 19.082
16000 15.301 539.67 0.45 0.58 0.41 0.37 -0.98 0.72 -0.48 20.359
17000 13.511 481.97 -0.65 -0.70 -0.12 -1.12 -1.35 1.57 0.06 21.635
18000 13.369 510.93 -1.23 -1.77 -1.05 -0.89 -1.19 0.50 -0.89 22.896
19000 14.594 496.53 -1.81 -2.12 -1.74 -1.58 -0.90 0.74 -1.54 24.173
20000 15.085 526.83 -0.78 -0.43 -1.62 -0.30 -0.67 0.92 -1.49 25.436
i,temperature = 4 600
sigma = 1.0e+00 bar
ttime = 20.000 fs
pfactor = 2000000.000 GPa*fs^2
log_filename = ./output/ch6/fcc-Cu_3x3x3_NPT_EMT_0600K.log
traj_filename = ./output/ch6/fcc-Cu_3x3x3_NPT_EMT_0600K.traj
imd Etot(eV) T(K) stress(mean,xx,yy,zz,yz,xz,xy)(GPa) elapsed_time(sec)
0 8.311 600.00 1.17 1.19 1.10 1.22 0.08 0.09 -0.13 0.002
1000 16.715 639.49 -5.01 -5.06 -5.46 -4.52 -0.26 -0.47 0.74 1.303
2000 15.139 488.07 -3.46 -3.57 -2.82 -3.99 0.14 -0.38 0.28 2.560
3000 15.724 510.99 -1.76 -1.63 -1.54 -2.11 0.32 0.23 0.14 3.810
4000 16.667 522.17 0.37 0.60 -0.06 0.57 -0.36 -0.75 1.05 5.093
5000 18.164 650.39 2.68 2.97 2.22 2.85 -0.26 -0.78 0.92 6.374
6000 18.164 554.33 3.50 3.53 2.99 3.97 -0.77 -0.83 0.67 7.659
7000 19.922 612.39 3.45 2.91 3.91 3.53 -0.73 -0.73 0.64 8.943
8000 19.457 526.47 2.56 2.06 3.09 2.53 -0.23 -0.41 -0.55 10.209
9000 18.140 513.53 1.80 1.78 1.80 1.83 -1.00 -0.53 0.31 11.515
10000 17.600 607.37 0.94 1.48 0.55 0.80 -1.20 -1.21 0.11 12.790
11000 16.172 524.88 -0.22 0.67 -0.72 -0.61 -0.27 -1.12 0.01 14.088
12000 18.702 704.78 -2.61 -3.05 -2.36 -2.43 0.12 -1.60 -0.33 15.368
13000 15.189 575.25 -2.38 -3.59 -1.61 -1.94 -0.24 -1.21 0.17 16.688
14000 16.155 612.83 -3.26 -3.77 -2.91 -3.10 -0.55 -0.88 -0.32 18.012
15000 16.451 596.63 -3.31 -2.66 -3.83 -3.43 0.09 -1.52 -0.10 19.394
16000 17.787 637.60 -2.79 -1.81 -3.53 -3.04 -0.18 -1.36 0.63 20.652
17000 17.834 671.97 -1.26 -1.60 -1.14 -1.05 -0.11 -1.15 0.35 21.921
18000 16.050 601.58 1.16 0.87 1.07 1.55 -0.44 -0.31 -0.03 23.190
19000 17.458 565.19 2.00 1.70 2.47 1.83 -0.77 -0.42 -0.06 24.472
20000 19.233 635.18 2.36 2.81 2.15 2.12 -0.59 -1.00 0.24 25.751
i,temperature = 5 700
sigma = 1.0e+00 bar
ttime = 20.000 fs
pfactor = 2000000.000 GPa*fs^2
log_filename = ./output/ch6/fcc-Cu_3x3x3_NPT_EMT_0700K.log
traj_filename = ./output/ch6/fcc-Cu_3x3x3_NPT_EMT_0700K.traj
imd Etot(eV) T(K) stress(mean,xx,yy,zz,yz,xz,xy)(GPa) elapsed_time(sec)
0 9.707 700.00 1.05 1.03 1.06 1.07 -0.08 -0.00 0.03 0.003
1000 20.383 739.14 -6.27 -5.74 -6.45 -6.63 0.11 0.36 -0.11 1.265
2000 19.614 696.89 -6.22 -5.47 -5.62 -7.56 0.29 0.43 -1.10 2.558
3000 17.879 652.89 -5.55 -5.02 -6.08 -5.54 0.78 0.43 -0.62 3.849
4000 19.976 694.34 -5.85 -6.30 -5.76 -5.50 1.30 0.36 -1.03 5.157
5000 20.035 673.12 -4.74 -5.06 -4.43 -4.75 1.29 0.12 -1.36 6.480
6000 20.622 645.33 -4.34 -4.75 -4.44 -3.84 0.60 0.24 -1.02 7.770
7000 19.666 627.41 -2.91 -2.72 -2.87 -3.16 0.41 -0.44 -1.34 9.066
8000 20.864 688.49 -2.25 -2.65 -1.63 -2.47 -0.17 -0.95 -1.13 10.364
9000 19.112 668.93 -0.62 -1.02 -0.78 -0.06 0.72 -0.62 -0.18 11.647
10000 20.284 699.50 -0.60 -1.47 -0.61 0.27 0.34 -0.59 -1.20 12.932
11000 19.498 697.73 0.77 1.59 0.63 0.10 1.27 0.18 0.07 14.195
12000 21.804 792.85 0.47 0.80 0.65 -0.04 -0.10 -0.18 0.28 15.469
13000 20.735 697.89 1.26 0.53 1.39 1.87 -0.02 1.01 0.63 16.741
14000 21.382 740.21 1.76 0.94 2.24 2.11 -0.77 0.17 0.04 18.031
15000 21.828 746.62 1.74 2.42 2.27 0.53 -0.53 -0.43 0.27 19.315
16000 22.004 746.30 1.52 1.97 1.16 1.41 -0.27 0.18 -0.14 20.603
17000 21.624 707.25 2.07 1.80 2.24 2.17 -0.22 -0.50 0.33 21.897
18000 21.128 685.74 2.77 2.07 2.31 3.92 -1.22 -1.43 0.32 23.188
19000 22.819 730.49 2.48 2.62 2.59 2.22 0.09 -1.54 0.20 24.495
20000 23.259 716.84 1.97 2.45 2.53 0.91 -1.07 -1.18 1.08 25.810
i,temperature = 6 800
sigma = 1.0e+00 bar
ttime = 20.000 fs
pfactor = 2000000.000 GPa*fs^2
log_filename = ./output/ch6/fcc-Cu_3x3x3_NPT_EMT_0800K.log
traj_filename = ./output/ch6/fcc-Cu_3x3x3_NPT_EMT_0800K.traj
imd Etot(eV) T(K) stress(mean,xx,yy,zz,yz,xz,xy)(GPa) elapsed_time(sec)
0 11.103 800.00 0.94 0.98 0.71 1.12 0.07 -0.06 0.09 0.003
1000 21.812 762.85 -6.73 -7.25 -6.65 -6.28 -1.23 -0.22 1.20 1.330
2000 23.271 804.18 -5.51 -6.51 -5.45 -4.57 -0.74 -2.03 2.05 2.610
3000 22.495 854.60 -4.24 -4.14 -4.29 -4.28 -0.35 -1.89 2.23 3.875
4000 22.232 796.81 -4.12 -3.80 -4.61 -3.94 0.86 -1.16 1.89 5.140
5000 19.335 764.45 -3.01 -3.04 -3.62 -2.37 1.60 -1.86 1.44 6.398
6000 21.821 797.04 -3.90 -4.50 -4.51 -2.71 1.97 -1.15 0.52 7.658
7000 21.947 772.94 -3.83 -3.48 -3.17 -4.83 1.76 0.10 -0.18 8.944
8000 21.421 765.09 -1.84 -0.79 -2.21 -2.52 0.80 0.48 -0.44 10.271
9000 22.487 823.21 -2.53 -1.80 -3.36 -2.43 0.48 0.16 0.25 11.551
10000 21.713 739.08 -1.72 -2.04 -1.70 -1.42 0.53 -0.28 0.16 12.830
11000 21.970 780.25 -0.64 -1.54 0.07 -0.45 -0.15 0.18 0.79 14.114
12000 21.425 665.58 -0.96 -1.23 -1.28 -0.35 0.06 0.38 -0.38 15.384
13000 20.883 650.72 0.13 0.77 -0.66 0.26 0.05 -0.42 0.02 16.655
14000 23.596 730.13 -0.27 -0.44 -0.71 0.35 -0.21 0.58 -1.00 17.939
15000 24.202 919.02 0.67 -0.22 0.52 1.70 0.82 0.45 -0.51 19.193
16000 24.128 778.05 0.16 -0.05 0.31 0.23 0.61 0.11 -0.13 20.468
17000 23.397 772.12 0.71 0.22 0.61 1.30 -0.09 0.09 0.26 21.757
18000 22.849 721.08 1.34 1.05 1.44 1.54 -0.17 0.64 1.09 23.043
19000 22.964 790.61 2.41 2.39 2.93 1.90 0.35 -0.16 -0.35 24.327
20000 24.617 749.05 1.23 1.33 1.37 1.00 0.72 0.06 0.23 25.591
i,temperature = 7 900
sigma = 1.0e+00 bar
ttime = 20.000 fs
pfactor = 2000000.000 GPa*fs^2
log_filename = ./output/ch6/fcc-Cu_3x3x3_NPT_EMT_0900K.log
traj_filename = ./output/ch6/fcc-Cu_3x3x3_NPT_EMT_0900K.traj
imd Etot(eV) T(K) stress(mean,xx,yy,zz,yz,xz,xy)(GPa) elapsed_time(sec)
0 12.499 900.00 0.82 0.81 0.90 0.75 0.10 -0.12 0.16 0.002
1000 23.423 834.16 -5.48 -6.79 -4.12 -5.52 -1.85 -0.69 1.58 1.337
2000 23.551 702.51 -2.86 -1.33 -3.18 -4.07 -1.04 -1.06 0.65 2.623
3000 27.744 907.63 0.38 0.00 -0.17 1.30 -0.08 -0.11 -0.75 3.884
4000 30.761 1002.33 3.16 2.31 3.78 3.40 -0.91 -0.75 -0.76 5.148
5000 33.001 998.32 2.50 2.02 3.62 1.87 0.09 -0.09 -0.45 6.405
6000 26.167 889.54 5.11 5.60 4.35 5.40 0.57 0.13 -0.48 7.676
7000 27.386 819.39 1.05 0.35 1.40 1.41 -0.35 -1.14 -0.54 8.949
8000 28.113 939.13 -0.24 -0.23 0.26 -0.75 -0.45 -0.45 0.91 10.217
9000 26.405 857.33 -0.70 0.41 -1.43 -1.08 -0.39 -0.53 0.79 11.499
10000 26.892 942.46 -1.89 -2.63 -2.42 -0.61 -0.14 -1.94 0.37 12.838
11000 28.269 995.74 -2.46 -3.68 -1.60 -2.09 -0.38 -1.49 0.73 14.126
12000 25.656 911.10 -1.00 -0.80 -0.72 -1.48 -0.10 -0.47 -0.16 15.392
13000 23.297 829.65 -0.23 0.43 -1.10 -0.02 -0.47 -0.32 -1.17 16.689
14000 25.628 898.60 0.28 0.51 0.28 0.03 -1.44 0.16 -1.20 17.956
15000 29.209 954.23 0.30 0.99 -0.21 0.13 -0.66 1.20 -1.12 19.225
16000 28.266 871.95 1.20 0.24 0.94 2.42 -0.44 0.29 -0.51 20.499
17000 28.500 866.69 1.15 0.89 1.41 1.17 -1.73 1.10 0.47 21.782
18000 27.243 832.05 -0.32 -0.36 -0.53 -0.06 -0.24 -0.07 0.67 23.041
19000 25.141 827.97 0.34 -0.02 -0.02 1.07 0.53 -0.12 0.41 24.301
20000 24.780 876.77 0.83 0.75 1.41 0.31 0.58 -0.45 -0.21 25.591
i,temperature = 8 1000
sigma = 1.0e+00 bar
ttime = 20.000 fs
pfactor = 2000000.000 GPa*fs^2
log_filename = ./output/ch6/fcc-Cu_3x3x3_NPT_EMT_1000K.log
traj_filename = ./output/ch6/fcc-Cu_3x3x3_NPT_EMT_1000K.traj
imd Etot(eV) T(K) stress(mean,xx,yy,zz,yz,xz,xy)(GPa) elapsed_time(sec)
0 13.895 1000.00 0.70 0.68 0.51 0.92 0.04 0.23 0.05 0.003
1000 29.676 928.19 -1.05 -1.83 0.19 -1.51 -1.12 0.72 -0.98 1.272
2000 33.128 1019.15 3.40 2.67 3.02 4.50 -0.63 1.02 -0.71 2.573
3000 35.329 1095.80 2.48 2.75 2.07 2.64 -1.08 1.38 -0.90 3.839
4000 31.810 1123.02 2.62 3.24 2.82 1.79 1.44 -0.16 -0.51 5.101
5000 32.830 1021.26 -2.58 -3.34 -2.37 -2.03 0.63 -0.60 3.17 6.380
6000 30.141 1113.73 -2.32 -2.18 -0.73 -4.04 -1.26 -1.62 1.31 7.648
7000 27.907 1047.10 -1.15 -0.14 -1.61 -1.71 -3.16 -1.67 1.65 8.931
8000 29.092 927.81 0.49 -0.38 -0.45 2.30 -1.93 -1.12 -0.04 10.200
9000 31.791 1071.16 0.44 0.48 0.67 0.18 -1.39 -0.41 -1.43 11.485
10000 30.929 1097.08 0.94 1.53 0.96 0.31 0.74 0.44 -0.87 12.740
11000 29.986 970.88 -0.02 -0.91 0.39 0.48 0.31 0.12 -0.64 14.001
12000 30.553 1083.88 -0.05 -0.12 0.48 -0.49 0.31 -0.27 -0.03 15.300
13000 30.370 994.91 -1.09 0.94 -2.24 -1.97 0.71 1.20 -0.35 16.600
14000 29.714 965.39 -0.41 -0.16 -0.50 -0.57 1.37 0.34 -0.07 17.892
15000 30.014 1041.61 0.15 0.29 -0.25 0.43 0.72 0.66 0.54 19.186
16000 30.035 1015.43 0.03 -0.76 0.76 0.07 0.17 0.29 -0.32 20.476
17000 29.797 963.30 0.34 0.45 -0.21 0.78 -1.20 -0.02 0.43 21.755
18000 30.446 962.12 0.94 1.05 0.33 1.44 -0.63 -0.22 1.30 23.051
19000 30.178 1023.73 0.53 0.16 0.66 0.77 0.18 -1.06 0.20 24.336
20000 29.661 950.11 -0.71 -1.22 -0.59 -0.33 -0.73 -2.03 0.06 25.601
A visualization of the results is shown below.
Here, the read method has been set to index="::100" to visualize the results of interval thinning from the Trajectory file. Although Cu retains its solid structure and is not moving significantly, we can see that there is a change in the cell size due to the vibrational movement.
[2]:
from ase.io import Trajectory, read
from pfcc_extras.visualize.povray import traj_to_apng
from IPython.display import Image
traj = read("./output/ch6/fcc-Cu_3x3x3_NPT_EMT_0900K.traj", index="::100")
traj_to_apng(traj, f"output/ch6/Fig6-3_fcc-Cu_3x3x3_NPT_EMT_0900K.png", rotation="10x,-10y,0z", clean=True, n_jobs=16)
Image(url="output/ch6/Fig6-3_fcc-Cu_3x3x3_NPT_EMT_0900K.png")
[Parallel(n_jobs=16)]: Using backend ThreadingBackend with 16 concurrent workers.
[Parallel(n_jobs=16)]: Done 12 out of 21 | elapsed: 5.8s remaining: 4.4s
[Parallel(n_jobs=16)]: Done 21 out of 21 | elapsed: 7.2s finished
[2]:
[3]:
from ase.io import Trajectory, read
from pfcc_extras.visualize.view import view_ngl
traj = read("./output/ch6/fcc-Cu_3x3x3_NPT_EMT_0900K.traj", index="::100")
view_ngl(traj, replace_structure=True)
[3]:
The time constant \(\tau_t\) of the heat bath is 20 fs and the barostat parameter, pfactor, is 2e6 GPa\(\cdot\)fs\(^2\). Let’s check how the cell volume changes with time during a 20 ps NPT-MD simulation at 300 K to achieve thermal equilibrium under the above calculation conditions. You can analyze the traj file, which is the result of MD simulation at a specific temperature, with the following code.
[4]:
import matplotlib.pyplot as plt
from pathlib import Path
from ase.io import read,Trajectory
time_step = 0.01 # Time step size in ps between each snapshots recorded in traj
traj = Trajectory("./output/ch6/fcc-Cu_3x3x3_NPT_EMT_0300K.traj")
time = [ i*time_step for i in range(len(traj)) ]
volume = [ atoms.get_volume() for atoms in traj ]
# Create graph
fig = plt.figure(figsize=(8,3))
ax = fig.add_subplot(1, 1, 1)
ax.set_xlabel('time (ps)') # x axis label
ax.set_ylabel('Cell volume (Å^3)') # y axis label
ax.plot(time,volume, alpha=0.5)
ax.set_ylim([1100,1400])
#plt.savefig("filename.png") # Set filename to be saved
plt.show()
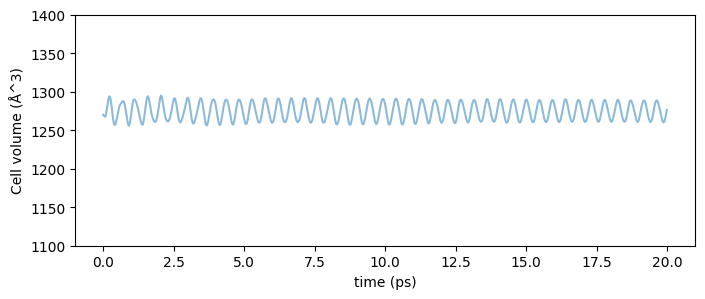
The time evolution of the cell volume for a 20 ps NPT-MD simulation at 300 K to achieve thermal equilibrium under these calculation conditions is shown below.
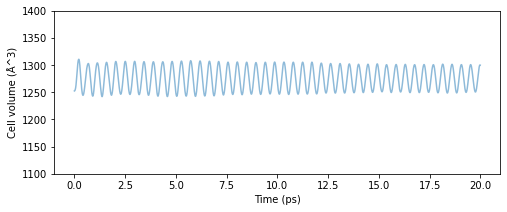
Fig.6-3a. Time evolution of cell volume. (fcc-Cu_3x3x3, @300 K and 1 bar)
It is shown that the cell volume oscillates within a range of about 4% with the NPT ensemble. Since we are dealing with cubic crystals, we can calculate the lattice constant of the crystal from the geometric mean of this volume, and by plotting the average normalized lattice constant at each temperature from 200 K to 1000 K, we obtain the following results. (Since we want to calculate the lattice constant after equilibrium is reached, we use only the second half of the Trajectory in the
np.mean(vol[int(len(vol)/2):])**(1/3) part to calculate the lattice constant from the volume.)
[5]:
import matplotlib.pyplot as plt
import numpy as np
from pathlib import Path
from ase.io import read,Trajectory
time_step = 10.0 # Time step size between each snapshots recorded in traj
paths = Path("./output/ch6/").glob(f"**/fcc-Cu_3x3x3_NPT_{calc_type}_*K.traj")
path_list = sorted([ p for p in paths ])
# Temperature list extracted from the filename
temperature = [ float(p.stem.split("_")[-1].replace("K","")) for p in path_list ]
print("temperature = ",temperature)
# Compute lattice parameter
lat_a = []
for path in path_list:
print(f"path = {path}")
traj = Trajectory(path)
vol = [ atoms.get_volume() for atoms in traj ]
lat_a.append(np.mean(vol[int(len(vol)/2):])**(1/3))
print("lat_a = ",lat_a)
# Normalize relative to the value at 300 K
norm_lat_a = lat_a/lat_a[1]
print("norm_lat_a = ",norm_lat_a)
# Plot
fig = plt.figure(figsize=(4,4))
ax = fig.add_subplot(1, 1, 1)
ax.set_xlabel('Temperature (K)') # x axis label
ax.set_ylabel('Normalized lattice parameter') # y axis label
ax.scatter(temperature[:len(norm_lat_a)],norm_lat_a, alpha=0.5,label=calc_type.lower())
ax.legend(loc="upper left")
temperature = [200.0, 300.0, 400.0, 500.0, 600.0, 700.0, 800.0, 900.0, 1000.0]
path = output/ch6/fcc-Cu_3x3x3_NPT_EMT_0200K.traj
path = output/ch6/fcc-Cu_3x3x3_NPT_EMT_0300K.traj
path = output/ch6/fcc-Cu_3x3x3_NPT_EMT_0400K.traj
path = output/ch6/fcc-Cu_3x3x3_NPT_EMT_0500K.traj
path = output/ch6/fcc-Cu_3x3x3_NPT_EMT_0600K.traj
path = output/ch6/fcc-Cu_3x3x3_NPT_EMT_0700K.traj
path = output/ch6/fcc-Cu_3x3x3_NPT_EMT_0800K.traj
path = output/ch6/fcc-Cu_3x3x3_NPT_EMT_0900K.traj
path = output/ch6/fcc-Cu_3x3x3_NPT_EMT_1000K.traj
lat_a = [10.821187657763522, 10.84284171781325, 10.866195382765163, 10.88834101681545, 10.91184951417741, 10.937661285868403, 10.958914931081702, 10.988423059467703, 11.016341565694251]
norm_lat_a = [0.99800292 1. 1.00215383 1.00419625 1.00636436 1.0087449
1.01070505 1.01342649 1.01600133]
[5]:
<matplotlib.legend.Legend at 0x7f2643b7a210>
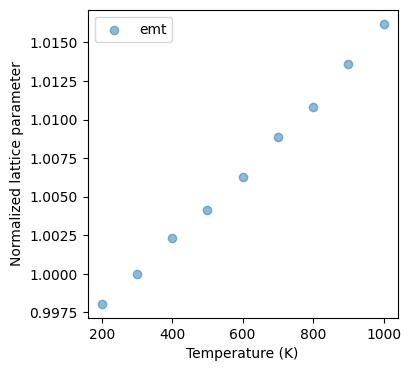
The following plot is obtained by running the above code.
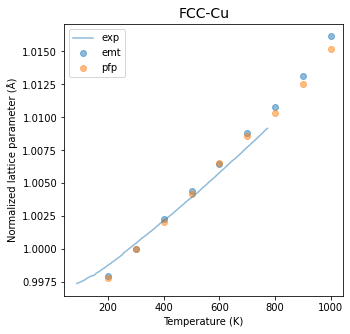
Fig.6-3b. Normalized lattice parameter as a function of temperature.
Experimental data is taken from Reference [4].
The results are further compared with the PFP calculations and, with the experimental data for reference. There is very good agreement for both the EMT and PFP data, while the PFP data appears to be closer to the experimental data with a small margin.
The coefficient of linear thermal expansion (CTE, \(\alpha\)) is calculated from the temperature dependence of the normalized lattice parameter using the following equation
where \(\alpha\) is the coefficient of linear thermal expansion and \(a(T)\) and \(a_{RT}\) are the lattice constants at temperature \(T\) and room temperature. The following is a summary of ASAP3-EMT, PFP, and experimental values [4].
\(\alpha\) ( \(10^{-5}\) /K) |
|
|---|---|
emt |
2.23 |
pfp |
2.13 |
exp |
1.74 |
Considering the calculation error, both calculation results are in reasonable agreement with the experimental values.
The coefficient of thermal expansion can be calculated by using MD simulations of the NPT ensemble in this way.
You may be thinking, “Can’t we reproduce thermal expansion of liquids and gases in the same way?” In principle, this is true, but at present there are only a limited number of models that can reproduce the thermal expansion of liquids and gases. There may be models that are specialized for specific liquids and gases in the classical force field, but when using first-principles calculations, the accuracy of intermolecular interactions in liquids and gases, which are much smaller than those in solids, is critical, and quantum chemical calculations with such accuracy are currently very difficult to perform. In particular, a large amount of computational data is required to create NNPs, and it is currently not very realistic to perform a large number of high-precision quantum chemical calculations. Therefore, the development of models with high accuracy in this area is expected in the future.
[Advanced] Parrinello-Rahman barostat parameter dependency¶
When performing MD simulations in the NPT ensemble, a parameter called pfactor needs to be chosen. It was explained that the appropriate value range is around 10\(^6\) GPa\(\cdot\)fs\(^2\) to 10\(^7\) GPa\(\cdot\)fs\(^2\). For your reference, the results when changing the value of pfactor are shown below. The calculation targets are the same fcc-Cu 3x3x3 unit cells as above, and the temperature is 300 K.
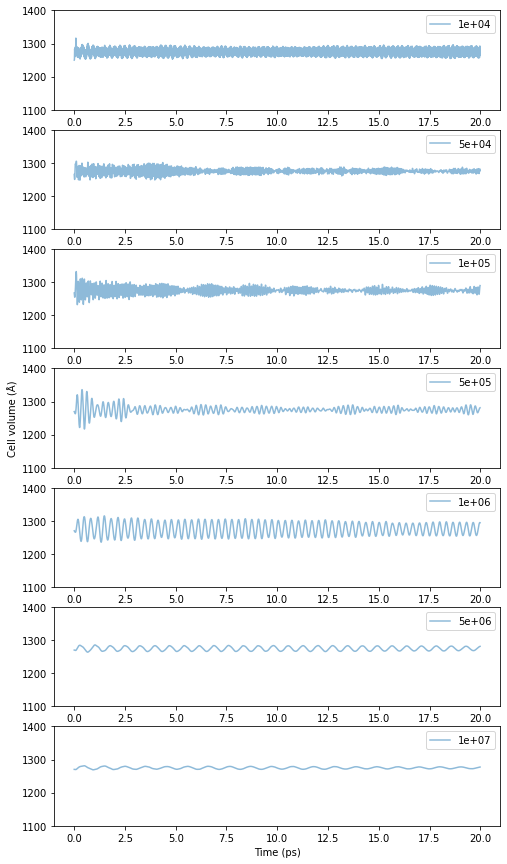
Fig.6-3c. Time evolution of cell volume as a function of pfactor.
When pfactor is small, the cell volume is oscillating at high speeds which is not desirable, and some regions have a mixture of high and low frequency oscillations making the system unstable. As pfactor increases, the period of oscillation gradually increases, and the large volume changes at the beginning of the calculation are hardly noticeable. Although there is no clear cut indicator of which value of pfactor is correct, the median value seems to be as stable as ever, although
small oscillations can be observed for values of 10\(^6\) Ga\(\cdot\)fsec\(^2\) or higher. Similarly, there is no well-defined reference for the upper limit, and since the larger the pfactor, the longer the oscillation period becomes and the more difficult it is to handle. A range between 10\(^6\) and 10\(^7\) seems appropriate for the above example.
[Advanced] Berendsen barostat parameter dependency¶
Here, we explain the calculation method using Berendsen barostat. The time evolution of pressure is calculated according to the following equation. (For details of the derivation, see reference [5]).
It is clear from the above equation that the Berendsen pressure control method exponentially increases the pressure at each time in the system closer to the external pressure \(\mathbf{P}_o\). Its speed is controlled by the time constant \(\tau_P\).
At each MD step, the coordinates and cell vectors of each atom are scaled by a factor expressed by the following equation
Just as \(\tau_T\) was a time constant when controlling a heat bath, an appropriate time constant \({\tau_P}\) must be set for the pressure control method. Let’s look at an actual calculation example.
Using the NPTBerendsen class, the object defining the dynamics is written in the following form
[6]:
from ase.md.nptberendsen import NPTBerendsen
dyn = NPTBerendsen(
atoms,
time_step*units.fs,
temperature_K = temperature,
pressure_au = 1.0 * units.bar,
taut = 5.0 * units.fs,
taup = 500.0 * units.fs,
compressibility_au = 5e-7 / units.bar,
logfile = log_filename,
trajectory = traj_filename,
loginterval=num_interval
)
Inhomogeneous_NPTBerendsen, which handles anisotropic pressure control, can be used with the same setting. (Simply relacing the class name from NPTBerendsen to Inhomogeneous_NPTBerendsen should work.) One difference between the two classes is that Inhomogeneous_NPTBerendsen accept mask argument can be set, i.e. setting mask=(1, 1, 1) allows the cell paramters a, b, and c can vary independently. If the element of this tuple is set to 0, the cell is fixed in that direction.
In addition to the calculation conditions such as temperature and pressure, it is necessary to set parameters called barostat time constant (taup, \(\tau_P\)) and compression ratio (compressibility, \(\beta_T\)). The dependence of the time variation of the cell volume on each of these values will be checked using the example of fcc-Cu at 300 K. We will start with \(\tau_P\).
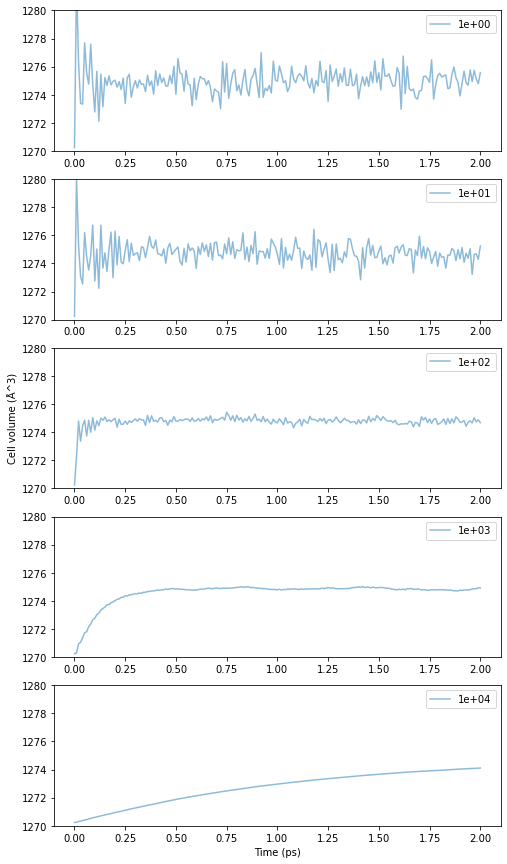
Fig.6-3d. Time evolution of cell volume as a function of \(\tau_P\).
The smaller the time constant, the more unstable and violent the period of oscillation is. On the other hand, if the time constant is too large, the change is too gradual and it takes time to reach equilibrium. This is the same concept as the time constant of the heat bath method. For a system mechanically similar to fcc-Cu, the appropriate value for \(\tau_P\) is around 10\(^2\) fs to 10\(^3\) fs due to the stability and convergence of the volume change.
Next is the dependence on \(\beta_T\). The results are as follows.
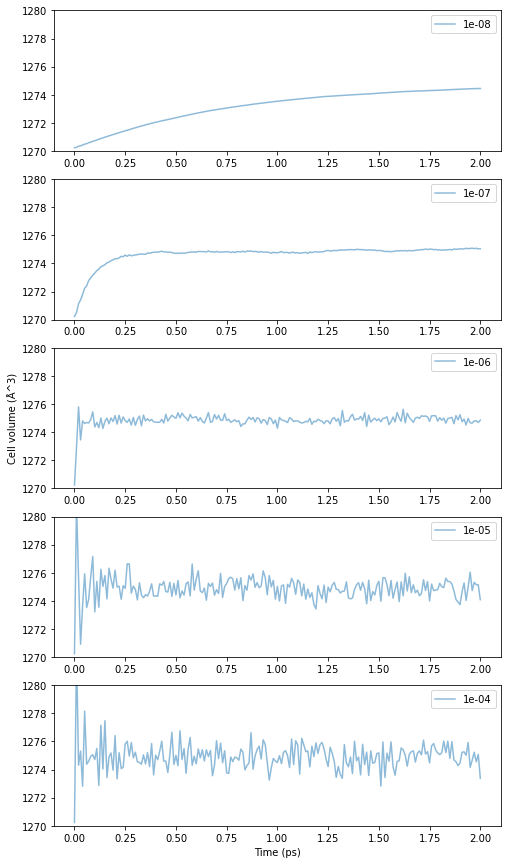
Fig.6-3e. Time evolution of cell volume as a function of \(\beta_T\).
The smaller \(\beta_T\) is, the slower the convergence is, and the higher the value, the more unstable it becomes. From the trend of the graph, 10\(^{-7}\) to 10\(^{-6}\)fs seems to be a good range for \(\beta_T\).
There is no strict guideline for choosing the values of \(\tau_P\) and \(\beta_T\). But it is better to have the sense of the trend when these values are changed by an order of magnitude.
Finally, it should be noted that these values are only applicable to dense metallic materials such as fcc-Cu. If one wants to treat a completely different kind of materials (e.g., polymers, liquids, gases, etc.) with NPT ensemble, the appropriate range of values should be studied in advance. In general, it is recommended that great care be taken when working with new material systems, as omitting this preliminary study may lead to unintended results and extra time.
Reference¶
[1] M.E. Tuckerman, “Statistical mechanics: Theory and molecular simulation”, Oxford University Press (2010) ISBN 978-0-19-852526-4. https://global.oup.com/academic/product/statistical-mechanics-9780198525264?q=Statistical%20mechanics:%20Theory%20and%20molecular%20simulation&cc=gb&lang=en#
[2] Melchionna S. (2000) “Constrained systems and statistical distribution”, Physical Review E 61 (6) 6165 https://journals.aps.org/pre/abstract/10.1103/PhysRevE.61.6165
[3] S. Melchionna, G. Ciccotti, B.L. Holian, “Hoover NPT dynamics for systems varying in shape and size”, Molecular Physics, (1993) 78 (3) 533 https://doi.org/10.1080/00268979300100371
[4] F.C. Nix, D. MacNair, “NIST:The Thermal Expansion of Pure Metals: Copper, Gold, Aluminum, Nickel, and Iron” https://materialsdata.nist.gov/handle/11256/32
[5] H. J. C. Berendsen, J. P. M. Postma, W. F. van Gunsteren, A. DiNola, and J. R. Haak, “Molecular dynamics with coupling to an external bath”, J. Chem. Phys. (1984) 81 3684 https://aip.scitation.org/doi/10.1063/1.448118