Atomistic simulation introduction

本Tutorialの扱う、”原子シミュレーション”とはどんなことができるものなのでしょうか？その概要を説明します。

材料のいろいろな性質は、原子レベルで説明することができます。例えば、機械的特性(弾性定数・ヤング率など)・熱物性(比熱など)・粘性・化学反応の起こりやすさ、、、などです。 原子シミュレーションを用いることで、原子を並べたときにどんな風に動くのかを再現したり、そもそも自然界ではどのように原子が並んでいるのかといったことを解析することができます。

説明は追って行うことにして、まずは以下のコードをそのまま流してみましょう。

Initial setup

Matlantis環境で以下のコマンドを実行することで、本Tutorialの実行に必要なライブラリをインストールできます。

  • pfp-api-client

  • matlantis-features

  • pfcc-extras

はMatlantis環境内で提供されているライブラリです。

※pfcc-extrasは、“Package Launcher”からフォルダをコピーし、内部のREADMEに従ってインストールを進めてください。 ※各ライブラリのインストール後、 インストールの反映にkernelの再起動が必要になる場合があります。インストールされたログが出たにもかかわらず、以降のimport が失敗する場合は、上部タブから“Restart kernel…”を選んでkernelの再起動をしてみてください。

[ ]:

!pip install -U pfp-api-client matlantis-features
# !pip install -e ../pfcc-extras  # please specify the path

MD simulationサンプルの実行

以下は、地表の主要な成分である二酸化ケイ素(SiO2結晶)に対してMD (分子動力学)シミュレーションを行うサンプルとなっています。

この時点で、コードの内容は全く理解できていなくて構いません。 「百聞は一見にしかず」ということで、まずは動かして可視化を行ってみます。 (本Tutorialを終える頃にはこのコードが何を行っているのか、簡単にわかるようになるでしょう。)

Input cif file is from
A. Jain, S.P. Ong, G. Hautier, W. Chen, W.D. Richards, S. Dacek, S. Cholia, D. Gunter, D. Skinner, G. Ceder, K.A. Persson (*=equal contributions)
The Materials Project: A materials genome approach to accelerating materials innovation APL Materials, 2013, 1(1), 011002.
doi:10.1063/1.4812323
[bibtex]
Licensed under CC BY 4.0
[2]:

from ase.md.velocitydistribution import MaxwellBoltzmannDistribution, Stationary
from ase.md.verlet import VelocityVerlet
from ase.optimize import BFGS
from ase.io import Trajectory, read
from ase import units

from pfp_api_client.pfp.calculators.ase_calculator import ASECalculator
from pfp_api_client.pfp.estimator import Estimator

estimator = Estimator()
calculator = ASECalculator(estimator)

atoms = read("../input/SiO2_mp-6930_conventional_standard.cif")
atoms.calc = calculator


opt = BFGS(atoms)
opt.run()

atoms = atoms * (3, 3, 3)
atoms.calc = calculator
# Set the momenta corresponding to T=700K.
MaxwellBoltzmannDistribution(atoms, temperature_K=700.0)
# Sets the center-of-mass momentum to zero.
Stationary(atoms)
# Run MD using the VelocityVerlet algorithm
dyn = VelocityVerlet(atoms, 1.0 * units.fs, trajectory="output/dyn.traj")

def print_dyn():
    print(f"Dyn  step: {dyn.get_number_of_steps(): >3}, energy: {atoms.get_total_energy():.3f}")

dyn.attach(print_dyn, interval=10)
dyn.run(100)

      Step     Time          Energy          fmax
BFGS:    0 06:22:44      -57.074789        0.015096
Dyn  step:   0, energy: -1517.819
Dyn  step:  10, energy: -1517.752
Dyn  step:  20, energy: -1517.766
Dyn  step:  30, energy: -1517.782
Dyn  step:  40, energy: -1517.764
Dyn  step:  50, energy: -1517.773
Dyn  step:  60, energy: -1517.776
Dyn  step:  70, energy: -1517.774
Dyn  step:  80, energy: -1517.769
Dyn  step:  90, energy: -1517.776
Dyn  step: 100, energy: -1517.778

[2]:

True

[3]:

from pfcc_extras.visualize.view import view_ngl

traj = Trajectory("output/dyn.traj")[::5]
view_ngl(traj, representations=["ball+stick"])

[4]:

from pfcc_extras.visualize.povray import traj_to_gif, traj_to_apng
from IPython.display import Image


traj_to_apng(traj, "output/sio2-md.png", rotation="30x,30y,30z", clean=True, n_jobs=16, width=600)
Image(url="output/sio2-md.png")  # , width=150

[Parallel(n_jobs=16)]: Using backend ThreadingBackend with 16 concurrent workers.
[Parallel(n_jobs=16)]: Done  12 out of  21 | elapsed:   39.4s remaining:   29.6s
[Parallel(n_jobs=16)]: Done  21 out of  21 | elapsed:   48.9s finished

[4]:

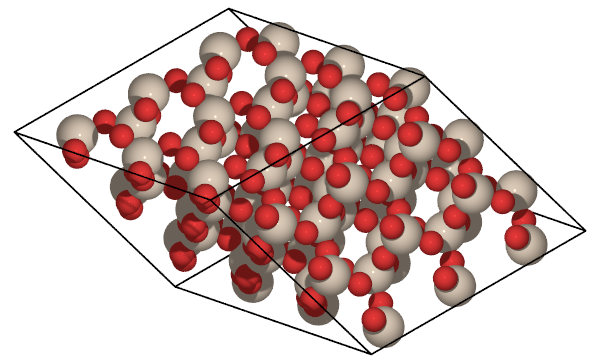
上記では分子動力学法とよばれる手法を用いることで、700K の温度環境下でSiO2 結晶の各原子がどのように動くのか、そのダイナミクスを追っています。

上記の例では243原子のシミュレーションを行いました。 体積で約\(3 \times 10^{-27}\)m、長さスケールでみると一辺約 15Å = (\(15 \times 10^{-10}\)m)であり、私達が日常生活で扱っている 1m スケールからすると桁違いにミクロな世界です。

ここで、検討しなければならないこととして、私達が扱っている材料をそのままのスケールでまるごとコンピュータ上でシミュレーションすることはできないということです。グラムオーダーの材料でもアボガドロ数、すなわち \(10^{23}\)オーダーの原子が存在しており、これだけの多くの数の原子をコンピュータ上で扱うことはできないためです。

そのため、原子シミュレーションでは、扱いたい現象に応じて適切なモデリング を行うことにより、自然界と全く同じものをつくりあげるのではなく、所望の現象を再現できるように必要な要素だけを抜き出しコンピュータ上で解析できるサイズの簡易化された系をつくりあげて、計算を進めていくことが必要になります。 モデリングには様々なノウハウが存在しますが、本チュートリアルを通して学んでいくことでできるようになってくるでしょう。

[コラム] モデリング

例えば、地球をシミュレーションしたいと考えたとき、もしも気象に興味があるのであれば地球表面の大気に注目したモデリングが必要になるでしょう。一方でもし地震に興味があれば大気よりも地球の内部構造に集中してモデル化する必要があります。もし地表の環境を再現したければ地球全体ではなく大陸の一部だけを切り出してきて考えることもあるでしょう。

再度、シミュレーション結果を見てみましょう。ここで登場するものは、以下のようなものがあります。

  • 原子

    • それぞれの原子が元素番号で指定され、xyz座標値をもち、速度を持っています

  • セル

    • 上記図では立方体で表現されている箱のことで、このセルが周期境界条件に従って無限に続くような系を扱うことができます。

真空中に浮いている分子のようなものを扱う場合には、セル・周期境界条件は必要ありません。 固体のように規則的な構造が続くような系は、周期境界条件を課すことでx, y, z軸(厳密には結晶軸となるa, b, c軸)それぞれの方向に無限に続くような構造を扱えます。

セル・周期境界条件というのは計算理論・モデリングの都合上の人工的な概念です。 結晶構造は、現実では内部で規則正しい構造が続き表面では別の構造をとっていると考えられますが、物質の表面は内部とは異なる特殊な状態であるため、水中や結晶のように物質の内部を扱いたい場合に表面を作ってしまうとしばしば不都合が生じます。そこで、セルという世界の限界を人工的に設定し、右端と左端がつながっているという周期境界条件を課すことによって、表面がなく繰り返し続いていく世界を作り出して問題を扱います。

次節から、こういった構造をPythonプログラムで扱い、原子シミュレーションを行う方法を学んでいきます。