振動解析 - Vibration Analysis¶
前章まででは、局所安定構造をもとめ、そこから得られる各種エネルギーを学びました。
本章では、安定構造周辺のエネルギー曲面 (PES: Potential Energy Surface)の挙動を解析することによって得られる物性を見ていきます。
まずは、周期境界のない系(有機分子など)に対する振動解析を行う、Vibrationを見ていきましょう。 振動解析によって得られる物性値は、IRスペクトルなど現実で観測できる量とも関連する物理量となります。
調和振動子近似 (Harmonic approximation)¶
これまでCalculatorを用いて求めてきた、ポテンシャルエネルギー \(V\) を、局所安定点の周りで近似することを考えてみましょう。
1変数関数 \(f(x)\) を、ある点\(x_0\) 周りで表すとテイラー展開を用いて、以下のように表せます。
ここで、\(\Delta x = x - x_0\) としています。
同様に、多変数関数 \(f(\mathbf{x})\)は、\(\Delta \mathbf{x} = \mathbf{x} - \mathbf{x_0}\) として、
と表せます。
ここで、ポテンシャルエネルギー \(V(\mathbf{r})\) に関してこの式を適用してみると、構造が安定となる点 \(\mathbf{r_0}\)では力 \(\mathbf{F}_i = \frac{\partial V(\mathbf{r_0})}{\partial r_i}\) が0となっているため、1次微分の項は0となり、2次までの展開では、
と書くことができます。
エネルギーの2回微分である \(\frac{\partial^2 V(\mathbf{r_0})}{\partial r_i \partial r_j}\)は、Hessianまたは、 力定数マトリクス(Force constant matrix) と呼ばれます。
このようにエネルギー曲面として、2次の項のみを考えるものは、バネにつながった系を考えた場合と同じエネルギーの形となり、調和振動子近似と呼びます。
以下の例は、5-9 調和振動子近似(*) – ページ 2 – Shinshu Univ., Physical Chemistry Lab., Adsorption Groupで示されているもので、 赤線のモースポテンシャル \(D(1-e^{- \beta x})^2\) を、x=0の安定点を中心にして青線の調和振動子ポテンシャル \((1/2)kx^2\) で近似した例を表します。\(x=0\) 付近では、近似がある程度成り立っていることがわかります。

図1: モースポテンシャル(赤線)と調和振動子ポテンシャル(青線)の比較 Shinshu Univ., Physical Chemistry Lab., Adsorption Group Iiyama & Futamura Laboratory より引用
Vibration¶
ポテンシャルエネルギー \(V(\mathbf{r})\) は\(N\)個の原子がある時、それぞれの原子に対して\(x, y, z\) の3方向に自由度を持つため、\(3N\) 次元関数となり、 Hessian \(\frac{\partial^2 V(\mathbf{r_0})}{\partial r_i \partial r_j}\) は \(3N \times 3N\) 次元の行列となります。 これを対角化することで、 \(3N\) 個の固有値と固有ベクトルが得られます。
それぞれの固有値がバネの強さ、固有ベクトルがバネの方向→振動モードに対応します。
\(3N\)個ある自由度の中で、分子全体が移動する並進運動の自由度が3、 また分子全体が重心を中心に回転する回転の自由度が直線分子では 2、非直線分子では 3 存在します。
最終的に、並進と回転の自由度をそれぞれ差し引いた以下の自由度の数だけ振動モード(基準振動)があります。
直線分子: \(3N-5\)
非直線分子: \(3N-6\)
実例を見ていきましょう。ASEでは Vibration moduleを使用することで振動解析を行うことが可能です。
H2O¶
H2Oは3原子からなる非直線分子なので、9個の自由度のうち、6個が並進・回転の自由度、3個が振動モードとなるはずです。
振動解析を行う際は、まず、系の構造最適化を行い、力が0になる点に移動させます。
[1]:
from ase.build import molecule
from ase.optimize import LBFGS, BFGS, FIRE
import pfp_api_client
from pfp_api_client.pfp.calculators.ase_calculator import ASECalculator
from pfp_api_client.pfp.estimator import Estimator, EstimatorCalcMode
estimator = Estimator(calc_mode=EstimatorCalcMode.PBE, model_version="v8.0.0")
calculator = ASECalculator(estimator)
atoms = molecule("H2O")
atoms.calc = calculator
LBFGS(atoms).run(fmax=0.0001)
Step Time Energy fmax
LBFGS: 0 05:45:02 -10.057427 0.207265
LBFGS: 1 05:45:02 -10.058143 0.083642
LBFGS: 2 05:45:02 -10.058258 0.045952
LBFGS: 3 05:45:02 -10.058402 0.013669
LBFGS: 4 05:45:02 -10.058406 0.003253
LBFGS: 5 05:45:02 -10.058407 0.000200
LBFGS: 6 05:45:02 -10.058407 0.000008
[1]:
True
ASEを用いる場合は Vibrationsを用いることにより、各振動モードの計算ができます。 この方法では、以下の式のように原子の位置を微小変化させた際の力の差分を求める事によりHessian を算出しています。
ここで、\(\Delta{r_i}\)は、\(3N\)個ある座標のうちi番目のみを微小変化させたベクトルを表します。
Vibrations moduleでは、 vib.run()で上記式の計算とその対角化を行い、vib.summary() で固有値のルートを出力しています。
vib.run()はnameで指定されたディレクトリを作成し、計算結果をキャッシュします。 そのため、別の計算を行う際にキャッシュファイルが残っていると新しい計算結果が反映されません。 キャッシュされたファイルの削除は、vib.clean()で行うことができます。
[2]:
from ase.vibrations import Vibrations
vib = Vibrations(atoms, indices=None, delta=0.01, name="vib-h2o", nfree=2)
vib.clean()
vib.run()
vib.summary()
---------------------
# meV cm^-1
---------------------
0 6.3i 50.9i
1 0.1i 0.6i
2 0.0i 0.2i
3 0.0i 0.1i
4 3.3 26.5
5 3.5 28.0
6 194.7 1570.3
7 459.0 3702.2
8 471.3 3800.9
---------------------
Zero-point energy: 0.566 eV
結果を見てみると、実際に並進・回転モードに対応する#0から#5までの6つのモードの固有エネルギーがほぼ0となっている事がわかります。 また、#6-#8の振動モードに対応する固有エネルギーは0より大きな値となっていることもわかります。
[Note]
“i” がついているものは虚数となっており、固有値がマイナスになっていることを表します。 これは2次関数で表した際に上に凸な2次曲面を表しており、更にエネルギーを下げる点が存在していることを示唆しており、構造最適化を行った局所安定点の振る舞いとしては望まれない結果となります。 ただし今回はその値は大きくないため、ほぼ0であるとみなすことができます。
各振動モードを可視化して見ましょう。
vib.write_mode()を用いると、カレントディレクトリ下に name で指定した名前で各振動モードのTrajectoryファイルが出力されます。
[3]:
for i in range(len(vib.get_energies())):
vib.write_mode(i)
以下のコードでは、modeの値を0から8に変えることで各振動モードがどのように振動しているかを確認することができます。
実際に、modeが0から5の値では並進や回転の運動となっていて、6から8の値を見ると、以下のように振動モードに対応していることがわかります。
mode 6: H2Oの角度が変わるような振動 (変角振動)
mode 7: HO間の結合長が同時に変わるような振動 (対称伸縮振動)
mode 8: HO間の結合長が交互に変わるような振動 (非対称伸縮振動)
以下の参考文献に記載されているようにそれぞれの振動をIRスペクトルで確認することもできます。
[4]:
from ase.io.trajectory import Trajectory
from pfcc_extras.visualize.view import view_ngl
mode = 6
traj = Trajectory(f"vib-h2o.{mode}.traj")
view_ngl(traj, representations=["ball+stick"])
[4]:
以下のようにして、各振動モードをアニメーション png ファイルとして保存することもできます。
[5]:
from tqdm.auto import tqdm
from pfcc_extras.visualize.povray import traj_to_apng
for mode in tqdm(range(9)):
traj = Trajectory(f"vib-h2o.{mode}.traj")
traj_to_apng(traj, f"output/vib-h2o.{mode}.png", rotation="90x,90y,180z", clean=True, n_jobs=16)
[Parallel(n_jobs=16)]: Using backend ThreadingBackend with 16 concurrent workers.
[Parallel(n_jobs=16)]: Done 30 out of 30 | elapsed: 2.4s finished
[Parallel(n_jobs=16)]: Using backend ThreadingBackend with 16 concurrent workers.
[Parallel(n_jobs=16)]: Done 30 out of 30 | elapsed: 2.5s finished
[Parallel(n_jobs=16)]: Using backend ThreadingBackend with 16 concurrent workers.
[Parallel(n_jobs=16)]: Done 30 out of 30 | elapsed: 2.7s finished
[Parallel(n_jobs=16)]: Using backend ThreadingBackend with 16 concurrent workers.
[Parallel(n_jobs=16)]: Done 30 out of 30 | elapsed: 2.3s finished
[Parallel(n_jobs=16)]: Using backend ThreadingBackend with 16 concurrent workers.
[Parallel(n_jobs=16)]: Done 30 out of 30 | elapsed: 2.6s finished
[Parallel(n_jobs=16)]: Using backend ThreadingBackend with 16 concurrent workers.
[Parallel(n_jobs=16)]: Done 30 out of 30 | elapsed: 2.3s finished
[Parallel(n_jobs=16)]: Using backend ThreadingBackend with 16 concurrent workers.
[Parallel(n_jobs=16)]: Done 30 out of 30 | elapsed: 2.4s finished
[Parallel(n_jobs=16)]: Using backend ThreadingBackend with 16 concurrent workers.
[Parallel(n_jobs=16)]: Done 30 out of 30 | elapsed: 2.5s finished
[Parallel(n_jobs=16)]: Using backend ThreadingBackend with 16 concurrent workers.
[Parallel(n_jobs=16)]: Done 30 out of 30 | elapsed: 2.4s finished
H2Oの振動モード
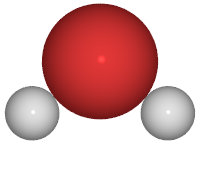
Mode #6
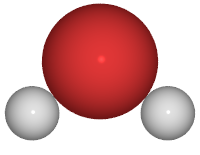
Mode #7
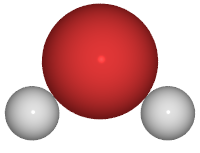
Mode #8
CO2¶
CO2はH2Oと同じ3原子からなりますが、直線分子です。 そのため、並進・回転モードが5つ、振動モードが4つになることが期待されます。
実際に確認してみましょう。前回同様、構造最適化を行ってから、振動解析を行います。
[6]:
atoms = molecule("CO2")
atoms.calc = calculator
LBFGS(atoms).run(fmax=0.001)
vib = Vibrations(atoms, indices=None, delta=0.01, name="vib-co2", nfree=2)
vib.clean()
vib.run()
vib.summary()
Step Time Energy fmax
LBFGS: 0 05:45:46 -17.747256 0.221567
LBFGS: 1 05:45:46 -17.747635 0.100589
LBFGS: 2 05:45:47 -17.747735 0.000831
---------------------
# meV cm^-1
---------------------
0 1.8i 14.9i
1 1.8i 14.9i
2 0.5i 4.0i
3 1.0 7.8
4 1.0 7.8
5 70.3 567.2
6 70.3 567.3
7 163.6 1319.2
8 289.5 2334.9
---------------------
Zero-point energy: 0.298 eV
[7]:
vib.write_mode()
実際に、#0-#4の並進・回転に相当する5つのモードで固有エネルギーがほぼ0となっており、#5-#8の振動に相当する固有モードが0より大きな値となっています。
前回同様可視化を行ってみます。#5と#6の振動は同じ固有エネルギーとなっていて、振動モード(=固有ベクトル)が縮退していることがわかります。
mode 5, 6: CO2の角度が変わるような振動、2つの方向への変化が縮退していることがわかります。
mode 7: CO間の結合長が同時に変わるような振動
mode 8: CO間の結合長が交互に変わるような振動
[8]:
from ase.io.trajectory import Trajectory
from pfcc_extras.visualize.view import view_ngl
mode = 5
traj = Trajectory(f"vib-co2.{mode}.traj")
view_ngl(traj, representations=["ball+stick"])
[8]:
[9]:
from tqdm.auto import tqdm
from pfcc_extras.visualize.povray import traj_to_apng
for mode in tqdm(range(9)):
traj = Trajectory(f"vib-co2.{mode}.traj")
traj_to_apng(traj, f"output/vib-co2.{mode}.png", rotation="30x,30y,30z", clean=True, n_jobs=16)
[Parallel(n_jobs=16)]: Using backend ThreadingBackend with 16 concurrent workers.
[Parallel(n_jobs=16)]: Done 30 out of 30 | elapsed: 2.4s finished
[Parallel(n_jobs=16)]: Using backend ThreadingBackend with 16 concurrent workers.
[Parallel(n_jobs=16)]: Done 30 out of 30 | elapsed: 2.6s finished
[Parallel(n_jobs=16)]: Using backend ThreadingBackend with 16 concurrent workers.
[Parallel(n_jobs=16)]: Done 30 out of 30 | elapsed: 2.5s finished
[Parallel(n_jobs=16)]: Using backend ThreadingBackend with 16 concurrent workers.
[Parallel(n_jobs=16)]: Done 30 out of 30 | elapsed: 2.8s finished
[Parallel(n_jobs=16)]: Using backend ThreadingBackend with 16 concurrent workers.
[Parallel(n_jobs=16)]: Done 30 out of 30 | elapsed: 2.8s finished
[Parallel(n_jobs=16)]: Using backend ThreadingBackend with 16 concurrent workers.
[Parallel(n_jobs=16)]: Done 30 out of 30 | elapsed: 2.5s finished
[Parallel(n_jobs=16)]: Using backend ThreadingBackend with 16 concurrent workers.
[Parallel(n_jobs=16)]: Done 30 out of 30 | elapsed: 2.3s finished
[Parallel(n_jobs=16)]: Using backend ThreadingBackend with 16 concurrent workers.
[Parallel(n_jobs=16)]: Done 30 out of 30 | elapsed: 2.4s finished
[Parallel(n_jobs=16)]: Using backend ThreadingBackend with 16 concurrent workers.
[Parallel(n_jobs=16)]: Done 30 out of 30 | elapsed: 2.3s finished
CO2の振動モード
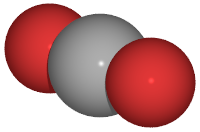
Mode #5
Mode #6
Mode #7
Mode #8
CH3OH¶
すこしだけ形を複雑にした分子として、CH3OHで同様に振動解析を行ってみます。
6個の原子を持つ非直線分子なので、最初の6つが並進・振動モードとなっており、残りの12個が振動モードとなっていることがわかります。
[10]:
atoms = molecule("CH3OH")
atoms.calc = calculator
LBFGS(atoms).run(fmax=0.001)
vib = Vibrations(atoms, indices=None, delta=0.01, name="vib-ch3oh", nfree=2)
vib.clean()
vib.run()
vib.summary()
Step Time Energy fmax
LBFGS: 0 05:46:25 -22.456031 0.265552
LBFGS: 1 05:46:25 -22.458848 0.160229
LBFGS: 2 05:46:25 -22.460468 0.072844
LBFGS: 3 05:46:25 -22.460642 0.067998
LBFGS: 4 05:46:25 -22.460903 0.025962
LBFGS: 5 05:46:25 -22.460962 0.020857
LBFGS: 6 05:46:26 -22.460994 0.017396
LBFGS: 7 05:46:26 -22.461026 0.017394
LBFGS: 8 05:46:26 -22.461047 0.009302
LBFGS: 9 05:46:26 -22.461054 0.008129
LBFGS: 10 05:46:26 -22.461057 0.006117
LBFGS: 11 05:46:26 -22.461057 0.007193
LBFGS: 12 05:46:26 -22.461058 0.003987
LBFGS: 13 05:46:26 -22.461058 0.001096
LBFGS: 14 05:46:26 -22.461063 0.000608
---------------------
# meV cm^-1
---------------------
0 1.5i 12.2i
1 0.9i 7.3i
2 0.1i 0.4i
3 0.0 0.3
4 0.1 0.7
5 0.8 6.3
6 37.3 300.5
7 123.8 998.8
8 129.9 1047.9
9 139.7 1127.0
10 163.7 1320.1
11 176.1 1420.2
12 179.1 1444.8
13 180.3 1453.9
14 361.0 2911.8
15 367.1 2960.7
16 376.9 3039.9
17 463.4 3737.8
---------------------
Zero-point energy: 1.350 eV
それぞれのモードを可視化して見てみましょう。モードによっては全体の原子が複雑に動くような振動モードも得られていることが確認できます。
[11]:
vib.write_mode()
[12]:
from ase.io.trajectory import Trajectory
from pfcc_extras.visualize.view import view_ngl
mode = 10
traj = Trajectory(f"vib-ch3oh.{mode}.traj")
view_ngl(traj, representations=["ball+stick"])
[12]:
CH4¶
最後に原子数が増えているが、対称性が高い分子の例として、CH4を見てみます。
5個の原子を持つ非直線分子なので、最初の6つが並進・回転モードとなっており、残りの9個が振動モードとなっていることがわかります。
[13]:
atoms = molecule("CH4")
atoms.calc = calculator
LBFGS(atoms).run(fmax=0.001)
vib = Vibrations(atoms, indices=None, delta=0.01, name="vib-ch4", nfree=2)
vib.clean()
vib.run()
vib.summary()
Step Time Energy fmax
LBFGS: 0 05:46:29 -18.196625 0.210110
LBFGS: 1 05:46:29 -18.198537 0.109506
LBFGS: 2 05:46:29 -18.199266 0.002115
LBFGS: 3 05:46:29 -18.199263 0.000019
---------------------
# meV cm^-1
---------------------
0 3.5i 28.3i
1 3.5i 28.3i
2 3.5i 28.3i
3 0.3i 2.2i
4 0.3i 2.2i
5 0.3i 2.2i
6 155.0 1250.3
7 155.0 1250.3
8 155.0 1250.3
9 185.3 1494.6
10 185.3 1494.6
11 367.3 2962.5
12 381.5 3076.9
13 381.5 3076.9
14 381.5 3076.9
---------------------
Zero-point energy: 1.174 eV
[14]:
vib.write_mode()
振動解析後に得られる物性値¶
振動解析の結果を利用することにより、例えば以下のような物性値が計算できます。
thermochemistry calculation: 理想気体近似などのもとで、enthalpyや自由エネルギーなどを求めることができます。詳しくは後ろの章で扱います。
IRスペクトルの波数: 振動解析の結果から、IR活性をもつ振動モードの吸収波数を特定できます。
[コラム] 調和振動子近似の有効範囲¶
本節で扱ったVibration、また次節で扱うPhononは調和振動子近似をもとに解析を進めていくため、この近似がどのような構造・場合において成り立つかを理解しておくことは大切です。 調和振動子近似は、安定構造付近のポテンシャルエネルギーをバネ型のPotential エネルギー \(1/2 k x^2\)で置き換えたものであり、下のイメージ図に示すように、各原子が原点からずれればずれるほど大きな力で原点に引き戻されるようなポテンシャルです。 すなわち、固体のように原子がその位置に留まるような構造では有効ですが、流体・気体のようにそもそも各原子が固定された場所に存在しないような場合は有効ではないことがわかります。
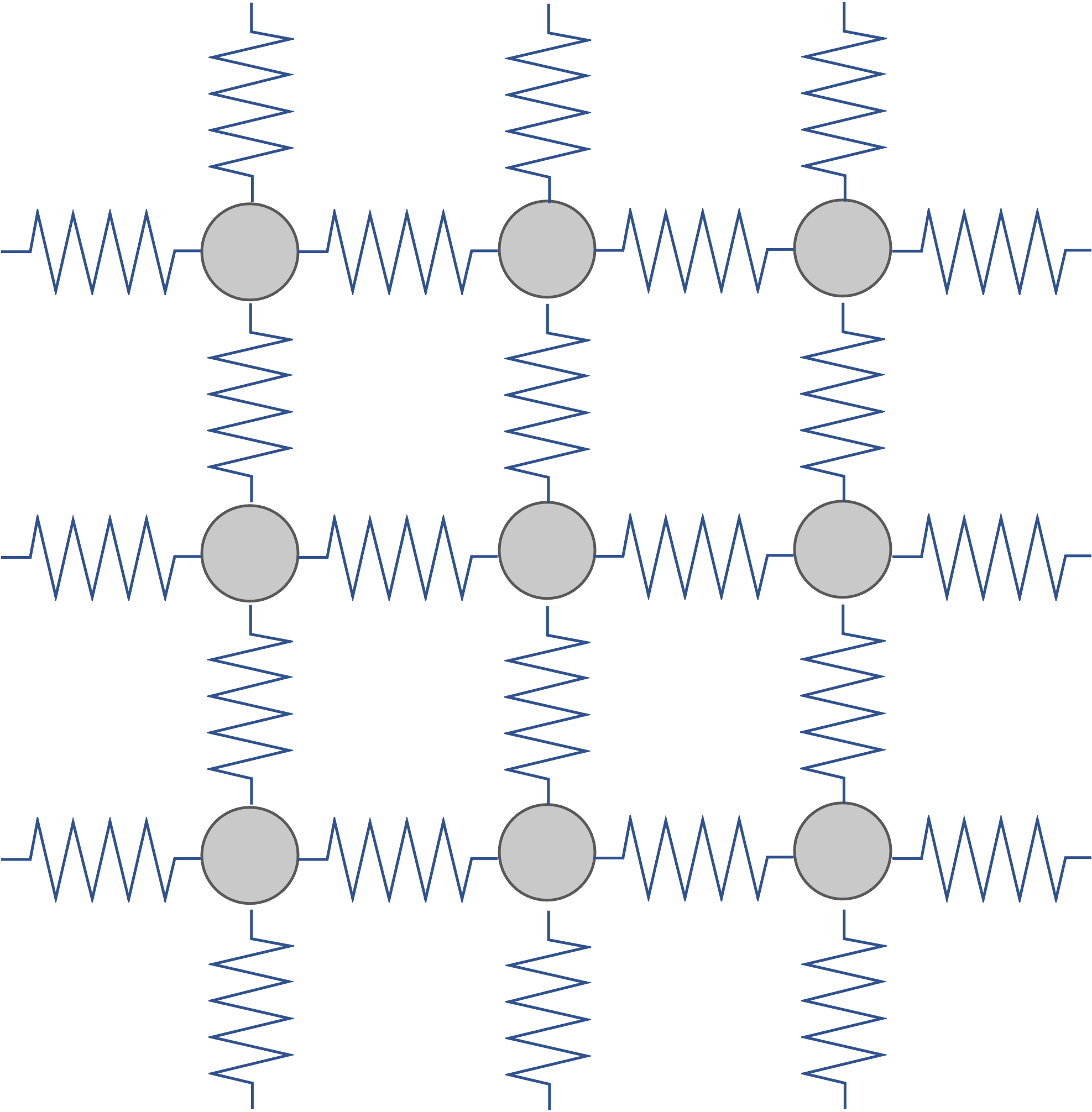
調和振動子近似が適用された原子系のイメージ図
これは温度とも関連します。物質が融点より高く液体状態になっている時は調和振動子近似は有効ではないと言えるでしょう。 目安として、融点に近づくと調和振動子近似の精度が大幅に下がり、低温領域でのみ有効な近似となります。
次節¶
本節では、分子などの周期境界条件のない系に対する振動解析を行いました。
次節では、結晶などの周期境界条件のある系に対する振動として得られる、 phononを扱います。