反応経路解析 - Reaction Path Analysis¶

前章まで安定構造付近の挙動を見ていましたが、いよいよ本章では、物質の反応を解析していきます。

X→Yへの反応に伴う、活性化エネルギー \(E_a\) と生成エンタルピー \(\Delta H\) の関係。 Wikipediaより。

ある反応物Xから生成物Yができる反応過程において、その反応経路中でエネルギーが最大となる点を 遷移状態 (TS: Transition State) と呼び、反応物・生成物から遷移状態までのエネルギー差を活性化エネルギー (Activation energy) \(E_a\) と呼びます。

アレニウスの式によると、反応の速度定数 \(k\) は、

\[k = A \exp \left(- \frac{E_a}{k_B T} \right)\]

で決まります。ここで、

\(A\): 頻度因子(温度に無関係な定数)
\(E_a\): 活性化エネルギー
\(k_B\): ボルツマン定数
\(T\): 絶対温度

です。つまり、化学反応の起こりやすさは活性化エネルギー \(E_a\) によって決まります。

反応物・生成物のエネルギーが変わることはありませんが、活性化エネルギーは周辺環境、つまり触媒の存在によって反応経路が変わることで変わります。この活性化エネルギーが低くなるような触媒を見つけられれば、対象とする反応をより起こしやすくすることができます。

参考文献

活性化エネルギー - Wikipedia
アレニウスの式 - Wikipedia
「分子レベルで見た触媒の働き　反応はなぜ速く進むのか」松本吉泰
「熱力学で理解する化学反応のしくみ」平山令明

反応物X、生成物Yがわかっていたとしても、遷移状態を見つけることは自明ではありません。本節では、反応前後の構造がわかっているときにその反応途中の経路を探索するNEB (Nudged Elastic Band)法を用いて、活性化エネルギーの算出を行ってみます。

https://databases.fysik.dtu.dk/ase/ase/neb.html

NEB¶

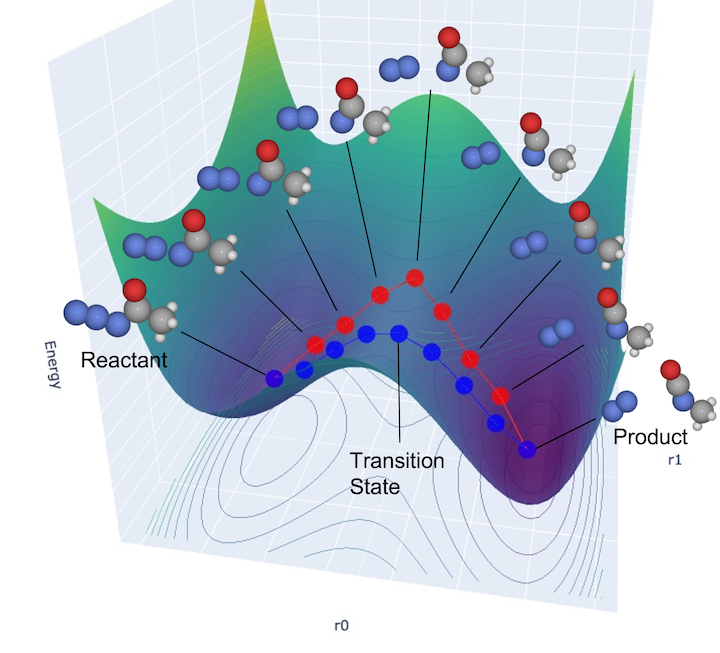
49c6ef96072d4254a4b4acd3125026f7 — NEB法のイメージ図: 初期配置として反応経路候補(赤線)を生成後、構造緩和を行い遷移状態を通るような反応経路(青線)を探索する

※ 以下の内容はMatlantis製品内に含まれるNEB Tutorialとほぼ同じ内容です。

今回は、クルチウス転位と呼ばれる有機化学反応の一例を題材にします。

NEB法では、ある注目したい反応についてその前後の構造からスタートしますが、今回は直接構造を書き下して構造を設定します。

[1]:

import numpy as np
from IPython.display import Image
import matplotlib.pyplot as plt

import ase
from ase import Atoms
from ase.visualize import view
from ase.optimize import BFGS
from ase.optimize import FIRE
from ase.neb import NEB
from ase.build.rotate import minimize_rotation_and_translation

from pfp_api_client.pfp.calculators.ase_calculator import ASECalculator
from pfp_api_client.pfp.estimator import Estimator
from pfp_api_client.pfp.estimator import Estimator, EstimatorCalcMode

estimator = Estimator(calc_mode=EstimatorCalcMode.PBE, model_version="v8.0.0")
calculator = ASECalculator(estimator)

[2]:

react = ase.Atoms(
    symbols="C2NON2H3",
    positions = [
        [ 2.12, -0.48,  0.00],
        [ 0.76,  0.16, -0.00],
        [-0.28, -0.79, -0.00],
        [ 0.57,  1.35,  0.00],
        [-1.42, -0.28,  0.00],
        [-2.48,  0.07,  0.00],
        [ 2.67, -0.14, -0.88],
        [ 2.06, -1.57, -0.00],
        [ 2.67, -0.14,  0.88],
    ],
)

prod = ase.Atoms(
    symbols="C2NON2H3",
    positions=[
        [ 2.30, -0.87,  0.00],
        [ 0.68,  0.92, -0.00],
        [ 0.99, -0.25,  0.00],
        [ 0.25,  2.03,  0.00],
        [-2.34,  0.11,  0.00],
        [-3.13, -0.67, -0.00],
        [ 2.87, -0.57, -0.89],
        [ 2.19, -1.96,  0.00],
        [ 2.87, -0.57,  0.89],
    ],
)

まずは構造最適化計算を行います。構造最適化計算のやり方は今までと同様です。

また、後の作業のため、minimize_rotation_and_translation methodを用いて、反応前後の2つの構造がなるべく近くなるように位置を移動させておきます。

[3]:

react.calc = calculator
opt = BFGS(react)
opt.run(fmax=0.01)

prod.calc = calculator
opt = BFGS(prod)
opt.run(fmax=0.01)

minimize_rotation_and_translation(react, prod)

      Step     Time          Energy          fmax
BFGS:    0 05:53:02      -41.413419        3.177696
BFGS:    1 05:53:07      -41.195533        8.812655
BFGS:    2 05:53:07      -41.470582        0.869362
BFGS:    3 05:53:07      -41.475647        0.802335
BFGS:    4 05:53:07      -41.480740        0.326584
BFGS:    5 05:53:07      -41.482541        0.187571
BFGS:    6 05:53:07      -41.484103        0.097033
BFGS:    7 05:53:08      -41.484652        0.066656
BFGS:    8 05:53:08      -41.485013        0.077300
BFGS:    9 05:53:08      -41.485479        0.091526
BFGS:   10 05:53:08      -41.485934        0.083387
BFGS:   11 05:53:08      -41.486403        0.071168
BFGS:   12 05:53:08      -41.486817        0.072329
BFGS:   13 05:53:08      -41.487162        0.050056
BFGS:   14 05:53:08      -41.487408        0.046723
BFGS:   15 05:53:08      -41.487569        0.033225
BFGS:   16 05:53:08      -41.487688        0.036092
BFGS:   17 05:53:08      -41.487823        0.039096
BFGS:   18 05:53:08      -41.487948        0.046989
BFGS:   19 05:53:08      -41.488031        0.031865
BFGS:   20 05:53:08      -41.488063        0.013554
BFGS:   21 05:53:09      -41.488073        0.012217
BFGS:   22 05:53:09      -41.488093        0.013953
BFGS:   23 05:53:09      -41.488106        0.019451
BFGS:   24 05:53:09      -41.488128        0.015627
BFGS:   25 05:53:09      -41.488135        0.006002
      Step     Time          Energy          fmax
BFGS:    0 05:53:09      -42.999059        0.928905
BFGS:    1 05:53:09      -42.979845        2.213718
BFGS:    2 05:53:09      -43.002931        0.183858
BFGS:    3 05:53:09      -43.002438        0.498714
BFGS:    4 05:53:09      -43.004179        0.132442
BFGS:    5 05:53:09      -43.005464        0.146250
BFGS:    6 05:53:09      -43.008521        0.384096
BFGS:    7 05:53:09      -43.011647        0.401999
BFGS:    8 05:53:10      -43.015385        0.276139
BFGS:    9 05:53:10      -43.018492        0.163363
BFGS:   10 05:53:10      -43.021307        0.250461
BFGS:   11 05:53:10      -43.023818        0.292535
BFGS:   12 05:53:10      -43.025384        0.156905
BFGS:   13 05:53:10      -43.026212        0.098028
BFGS:   14 05:53:10      -43.026830        0.146643
BFGS:   15 05:53:10      -43.027199        0.128298
BFGS:   16 05:53:10      -43.027410        0.062755
BFGS:   17 05:53:10      -43.027560        0.069153
BFGS:   18 05:53:10      -43.027842        0.149047
BFGS:   19 05:53:10      -43.028350        0.228853
BFGS:   20 05:53:10      -43.029111        0.244633
BFGS:   21 05:53:11      -43.030054        0.159354
BFGS:   22 05:53:11      -43.031161        0.120736
BFGS:   23 05:53:11      -43.032580        0.200826
BFGS:   24 05:53:11      -43.034554        0.315799
BFGS:   25 05:53:11      -43.036725        0.259742
BFGS:   26 05:53:11      -43.037638        0.081485
BFGS:   27 05:53:11      -43.037804        0.026730
BFGS:   28 05:53:11      -43.037886        0.024726
BFGS:   29 05:53:11      -43.037905        0.020094
BFGS:   30 05:53:11      -43.037905        0.007461

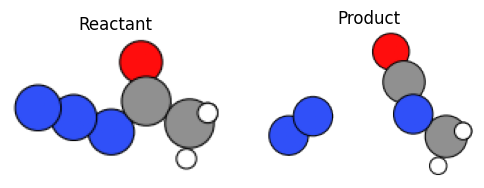
可視化を行い、反応前後の構造を確認します。

[4]:

from ase.io import write
from IPython.display import Image
import matplotlib.pyplot as plt
import matplotlib.image as mpimg

write("output/curtius_react.png", react, rotation="0x,0y,0z")
write("output/curtius_prod.png", prod, rotation="0x,0y,0z")

fig, axes = plt.subplots(1, 2, figsize=(6, 3))
ax0, ax1 = axes
ax0.imshow(mpimg.imread("output/curtius_react.png"))
ax0.set_axis_off()
ax0.set_title("Reactant")
ax1.imshow(mpimg.imread("output/curtius_prod.png"))
ax1.set_axis_off()
ax1.set_title("Product")
fig.show()

[5]:

from pfcc_extras.visualize.view import view_ngl

view_ngl([react, prod], representations=["ball+stick"], replace_structure=True)

[5]:

ここからがNEB法の出番です。NEB法は、反応の前後の構造を離散的に補完した構造を多数用意し、それら複数の構造を位相空間上で互いに結合させつつ構造最適化を行うことで反応経路を探す手法です。

中間点の補完やNEBの実行そのもののはASEの組み込みのものを使うことができます。以下の例のように、allow_shared_calculator=Falseを指定し、各 image に対して個別のCalculatorをセットすることで高速化が可能です。

NEBは複数の構造を内部で使う手法のため、MD計算などと比較するとステップあたりの計算時間は大きくなります。従来、DFTなどの量子計算手法を用いる場合は数日から数ヶ月かかることもありますが、Matlantisでは本例では数分とかからずに終わらせることができます。

計算は以下のようなステップで行われています。

まず images としてASE Atomsのリストを作成します。
- 最初が反応物 reactで、最後が生成物 prod になるようにします。
- 中間 image は後の neb.interpolate() で座標値が変更されるので、ここではコピーを作成しておきます。
- 今回は、中間 imageを7つ、合計9つで images を作成しました。
それぞれの Atoms に対して calculator を作成し、セットします。
NEBクラスを作成します。
- kが各 imagesをつなげるバネの強さを表すバネ定数です
- climb=True とすることで、Climbing Image NEB法と呼ばれる、遷移状態を見つけるためにエネルギー勾配を上る手法を用いています。
neb.interpolate()
- ここで images の線形補間をおこない、生成物から反応物へ座標が徐々に変わるようなリストを作成しています。
- この時点で生成された反応経路の初期配置(候補)は、コメントアウトしてある view_ngl の可視化を行うことで、確認できます。
FIREでopt
- 得られた反応経路候補をFIRE法を用いて最適化することで、適切な反応経路に修正していきます。

[6]:

images = [react.copy()]
images += [react.copy() for i in range (7)]
images += [prod.copy()]
for image in images:
    estimator = Estimator(calc_mode=EstimatorCalcMode.PBE, model_version="v8.0.0")
    calculator = ASECalculator(estimator)
    image.calc = calculator
neb = NEB(images, k=0.1, climb=True, allow_shared_calculator=False, parallel=True)
neb.interpolate()
# Check interpolated images
# view_ngl(images, representations=["ball+stick"], replace_structure=True)
opt = FIRE(neb)
status = opt.run(fmax=0.05, steps=500)

      Step     Time          Energy          fmax
FIRE:    0 05:53:17      -36.039934       51.039993

/tmp/ipykernel_38727/1903780971.py:8: FutureWarning: Please import NEB from ase.mep, not ase.neb.
  neb = NEB(images, k=0.1, climb=True, allow_shared_calculator=False, parallel=True)

FIRE:    1 05:53:17      -38.793782        9.718599
FIRE:    2 05:53:18      -38.639883       11.420030
FIRE:    3 05:53:18      -39.024515        7.290823
FIRE:    4 05:53:18      -39.146942        7.625532
FIRE:    5 05:53:18      -39.187412        5.992777
FIRE:    6 05:53:18      -39.239850        3.735237
FIRE:    7 05:53:18      -39.275642        3.622289
FIRE:    8 05:53:18      -39.291292        3.493045
FIRE:    9 05:53:18      -39.304292        4.473294
FIRE:   10 05:53:19      -39.331143        4.526304
FIRE:   11 05:53:19      -39.372896        3.701372
FIRE:   12 05:53:19      -39.419352        2.238812
FIRE:   13 05:53:19      -39.443115        2.080150
FIRE:   14 05:53:19      -39.440229        3.654853
FIRE:   15 05:53:19      -39.444635        2.844699
FIRE:   16 05:53:19      -39.441267        1.513861
FIRE:   17 05:53:19      -39.386240        2.479679
FIRE:   18 05:53:20      -39.331586        1.880054
FIRE:   19 05:53:20      -39.281403        1.779987
FIRE:   20 05:53:20      -39.283645        1.548858
FIRE:   21 05:53:20      -39.287574        1.518645
FIRE:   22 05:53:20      -39.292569        1.468452
FIRE:   23 05:53:20      -39.298437        1.397878
FIRE:   24 05:53:20      -39.305505        1.310686
FIRE:   25 05:53:20      -39.314064        1.211725
FIRE:   26 05:53:21      -39.323960        1.103863
FIRE:   27 05:53:21      -39.335856        0.975578
FIRE:   28 05:53:21      -39.349554        0.838575
FIRE:   29 05:53:21      -39.365411        0.882636
FIRE:   30 05:53:21      -39.383477        0.645287
FIRE:   31 05:53:21      -39.402059        0.823016
FIRE:   32 05:53:21      -39.419176        0.710753
FIRE:   33 05:53:21      -39.432073        0.612654
FIRE:   34 05:53:22      -39.435664        0.673938
FIRE:   35 05:53:22      -39.429984        0.665475
FIRE:   36 05:53:22      -39.417316        0.741882
FIRE:   37 05:53:22      -39.409039        0.755364
FIRE:   38 05:53:22      -39.416518        0.662316
FIRE:   39 05:53:22      -39.450880        0.688317
FIRE:   40 05:53:22      -39.504750        1.002623
FIRE:   41 05:53:22      -39.531253        1.980011
FIRE:   42 05:53:22      -39.531704        1.053129
FIRE:   43 05:53:23      -39.515310        1.783475
FIRE:   44 05:53:23      -39.516177        1.343500
FIRE:   45 05:53:23      -39.516109        0.887946
FIRE:   46 05:53:23      -39.513257        0.844553
FIRE:   47 05:53:23      -39.507936        0.981732
FIRE:   48 05:53:23      -39.502429        1.231033
FIRE:   49 05:53:23      -39.498270        1.107979
FIRE:   50 05:53:23      -39.495246        0.670416
FIRE:   51 05:53:24      -39.491761        0.478543
FIRE:   52 05:53:24      -39.487278        0.836828
FIRE:   53 05:53:24      -39.484502        0.931134
FIRE:   54 05:53:24      -39.485000        0.400947
FIRE:   55 05:53:24      -39.486132        0.687748
FIRE:   56 05:53:24      -39.488696        0.821196
FIRE:   57 05:53:24      -39.494420        0.299127
FIRE:   58 05:53:24      -39.498288        0.816078
FIRE:   59 05:53:25      -39.498931        0.651060
FIRE:   60 05:53:25      -39.499640        0.370306
FIRE:   61 05:53:25      -39.499844        0.387021
FIRE:   62 05:53:25      -39.499683        0.589927
FIRE:   63 05:53:25      -39.499753        0.568230
FIRE:   64 05:53:25      -39.499868        0.526476
FIRE:   65 05:53:25      -39.500018        0.468053
FIRE:   66 05:53:25      -39.500167        0.398406
FIRE:   67 05:53:26      -39.500278        0.325589
FIRE:   68 05:53:26      -39.500354        0.260600
FIRE:   69 05:53:26      -39.500395        0.295316
FIRE:   70 05:53:26      -39.500428        0.356153
FIRE:   71 05:53:26      -39.500498        0.391886
FIRE:   72 05:53:26      -39.500609        0.391706
FIRE:   73 05:53:26      -39.500797        0.348149
FIRE:   74 05:53:26      -39.501020        0.262223
FIRE:   75 05:53:26      -39.501209        0.304671
FIRE:   76 05:53:27      -39.501368        0.373761
FIRE:   77 05:53:27      -39.501593        0.386780
FIRE:   78 05:53:27      -39.501939        0.319477
FIRE:   79 05:53:27      -39.502316        0.236664
FIRE:   80 05:53:27      -39.502740        0.306992
FIRE:   81 05:53:27      -39.503442        0.221052
FIRE:   82 05:53:27      -39.504365        0.286691
FIRE:   83 05:53:28      -39.505714        0.257210
FIRE:   84 05:53:28      -39.507617        0.223562
FIRE:   85 05:53:28      -39.510176        0.142952
FIRE:   86 05:53:28      -39.513237        0.251855
FIRE:   87 05:53:28      -39.516656        0.249104
FIRE:   88 05:53:28      -39.519980        0.291716
FIRE:   89 05:53:28      -39.522918        0.423171
FIRE:   90 05:53:28      -39.525657        0.933060
FIRE:   91 05:53:28      -39.525950        0.122988
FIRE:   92 05:53:29      -39.526037        0.827977
FIRE:   93 05:53:29      -39.526125        0.630574
FIRE:   94 05:53:29      -39.526228        0.290080
FIRE:   95 05:53:29      -39.526321        0.146086
FIRE:   96 05:53:29      -39.526328        0.139804
FIRE:   97 05:53:29      -39.526347        0.127774
FIRE:   98 05:53:29      -39.526365        0.111241
FIRE:   99 05:53:29      -39.526388        0.109090
FIRE:  100 05:53:30      -39.526415        0.108170
FIRE:  101 05:53:30      -39.526451        0.107064
FIRE:  102 05:53:35      -39.526499        0.105773
FIRE:  103 05:53:35      -39.526544        0.112183
FIRE:  104 05:53:35      -39.526615        0.116831
FIRE:  105 05:53:35      -39.526700        0.118117
FIRE:  106 05:53:35      -39.526804        0.114901
FIRE:  107 05:53:35      -39.526934        0.107102
FIRE:  108 05:53:36      -39.527096        0.096492
FIRE:  109 05:53:36      -39.527287        0.098161
FIRE:  110 05:53:36      -39.527524        0.105876
FIRE:  111 05:53:36      -39.527818        0.109156
FIRE:  112 05:53:36      -39.528161        0.108226
FIRE:  113 05:53:36      -39.528585        0.107816
FIRE:  114 05:53:36      -39.529099        0.114348
FIRE:  115 05:53:36      -39.529700        0.128953
FIRE:  116 05:53:37      -39.530423        0.141629
FIRE:  117 05:53:37      -39.531288        0.141220
FIRE:  118 05:53:37      -39.532314        0.137819
FIRE:  119 05:53:37      -39.533546        0.148716
FIRE:  120 05:53:37      -39.535015        0.148140
FIRE:  121 05:53:37      -39.536748        0.124585
FIRE:  122 05:53:37      -39.538754        0.141570
FIRE:  123 05:53:37      -39.540931        0.334313
FIRE:  124 05:53:38      -39.542964        0.872740
FIRE:  125 05:53:38      -39.543108        0.099246
FIRE:  126 05:53:38      -39.543123        0.801354
FIRE:  127 05:53:38      -39.543166        0.608250
FIRE:  128 05:53:38      -39.543222        0.276952
FIRE:  129 05:53:38      -39.543266        0.167962
FIRE:  130 05:53:38      -39.543263        0.159837
FIRE:  131 05:53:38      -39.543266        0.144121
FIRE:  132 05:53:39      -39.543273        0.121977
FIRE:  133 05:53:39      -39.543288        0.108850
FIRE:  134 05:53:39      -39.543294        0.097559
FIRE:  135 05:53:39      -39.543311        0.086447
FIRE:  136 05:53:39      -39.543328        0.090467
FIRE:  137 05:53:39      -39.543352        0.099416
FIRE:  138 05:53:39      -39.543379        0.105308
FIRE:  139 05:53:40      -39.543413        0.106516
FIRE:  140 05:53:40      -39.543449        0.101807
FIRE:  141 05:53:40      -39.543505        0.091059
FIRE:  142 05:53:40      -39.543559        0.084905
FIRE:  143 05:53:40      -39.543637        0.096808
FIRE:  144 05:53:40      -39.543725        0.101426
FIRE:  145 05:53:40      -39.543840        0.093861
FIRE:  146 05:53:40      -39.543970        0.076909
FIRE:  147 05:53:41      -39.544133        0.090605
FIRE:  148 05:53:41      -39.544324        0.085783
FIRE:  149 05:53:41      -39.544556        0.078244
FIRE:  150 05:53:41      -39.544833        0.084897
FIRE:  151 05:53:41      -39.545156        0.070795
FIRE:  152 05:53:41      -39.545549        0.080475
FIRE:  153 05:53:41      -39.546006        0.079829
FIRE:  154 05:53:41      -39.546542        0.066319
FIRE:  155 05:53:42      -39.547176        0.067482
FIRE:  156 05:53:42      -39.547931        0.083006
FIRE:  157 05:53:42      -39.548789        0.205813
FIRE:  158 05:53:42      -39.549665        0.591954
FIRE:  159 05:53:42      -39.549807        0.069105
FIRE:  160 05:53:42      -39.549764        0.546293
FIRE:  161 05:53:42      -39.549809        0.415580
FIRE:  162 05:53:42      -39.549869        0.190804
FIRE:  163 05:53:42      -39.549892        0.139658
FIRE:  164 05:53:43      -39.549892        0.133200
FIRE:  165 05:53:43      -39.549899        0.120721
FIRE:  166 05:53:43      -39.549903        0.103139
FIRE:  167 05:53:43      -39.549910        0.081804
FIRE:  168 05:53:43      -39.549919        0.073125
FIRE:  169 05:53:43      -39.549927        0.066290
FIRE:  170 05:53:43      -39.549937        0.068883
FIRE:  171 05:53:43      -39.549953        0.079353
FIRE:  172 05:53:43      -39.549967        0.090279
FIRE:  173 05:53:44      -39.549984        0.092056
FIRE:  174 05:53:44      -39.550013        0.082493
FIRE:  175 05:53:44      -39.550042        0.069312
FIRE:  176 05:53:49      -39.550080        0.068212
FIRE:  177 05:53:49      -39.550123        0.076010
FIRE:  178 05:53:49      -39.550180        0.079268
FIRE:  179 05:53:49      -39.550251        0.075107
FIRE:  180 05:53:50      -39.550338        0.064926
FIRE:  181 05:53:50      -39.550441        0.074295
FIRE:  182 05:53:50      -39.550568        0.070558
FIRE:  183 05:53:50      -39.550722        0.070874
FIRE:  184 05:53:50      -39.550914        0.076569
FIRE:  185 05:53:50      -39.551142        0.064690
FIRE:  186 05:53:50      -39.551415        0.071405
FIRE:  187 05:53:50      -39.551746        0.075358
FIRE:  188 05:53:51      -39.552141        0.063727
FIRE:  189 05:53:51      -39.552616        0.065579
FIRE:  190 05:53:51      -39.553177        0.080591
FIRE:  191 05:53:51      -39.553823        0.147884
FIRE:  192 05:53:51      -39.554451        0.450631
FIRE:  193 05:53:51      -39.553907        1.523635
FIRE:  194 05:53:51      -39.555313        0.447544
FIRE:  195 05:53:51      -39.555376        0.315242
FIRE:  196 05:53:51      -39.555435        0.099751
FIRE:  197 05:53:52      -39.555439        0.194017
FIRE:  198 05:53:52      -39.555440        0.181617
FIRE:  199 05:53:52      -39.555446        0.157913
FIRE:  200 05:53:52      -39.555456        0.125072
FIRE:  201 05:53:52      -39.555471        0.086514
FIRE:  202 05:53:52      -39.555472        0.068387
FIRE:  203 05:53:52      -39.555480        0.078347
FIRE:  204 05:53:52      -39.555495        0.096848
FIRE:  205 05:53:53      -39.555500        0.116901
FIRE:  206 05:53:53      -39.555517        0.122322
FIRE:  207 05:53:53      -39.555533        0.109575
FIRE:  208 05:53:53      -39.555560        0.083278
FIRE:  209 05:53:53      -39.555590        0.068323
FIRE:  210 05:53:53      -39.555622        0.086235
FIRE:  211 05:53:53      -39.555661        0.106219
FIRE:  212 05:53:53      -39.555713        0.088472
FIRE:  213 05:53:54      -39.555770        0.066366
FIRE:  214 05:53:54      -39.555843        0.089731
FIRE:  215 05:53:59      -39.555933        0.084281
FIRE:  216 05:53:59      -39.556047        0.067116
FIRE:  217 05:53:59      -39.556168        0.094122
FIRE:  218 05:53:59      -39.556329        0.065264
FIRE:  219 05:53:59      -39.556516        0.087438
FIRE:  220 05:54:00      -39.556739        0.085869
FIRE:  221 05:54:00      -39.556995        0.061607
FIRE:  222 05:54:00      -39.557304        0.072056
FIRE:  223 05:54:00      -39.557650        0.132123
FIRE:  224 05:54:00      -39.557982        0.334818
FIRE:  225 05:54:00      -39.558004        0.891905
FIRE:  226 05:54:00      -39.558459        0.098080
FIRE:  227 05:54:00      -39.558466        0.077496
FIRE:  228 05:54:01      -39.558469        0.059984
FIRE:  229 05:54:01      -39.558473        0.058698
FIRE:  230 05:54:01      -39.558484        0.074467
FIRE:  231 05:54:01      -39.558490        0.081043
FIRE:  232 05:54:01      -39.558506        0.071273
FIRE:  233 05:54:01      -39.558525        0.056332
FIRE:  234 05:54:01      -39.558543        0.059079
FIRE:  235 05:54:01      -39.558569        0.067035
FIRE:  236 05:54:02      -39.558596        0.061212
FIRE:  237 05:54:02      -39.558629        0.053757
FIRE:  238 05:54:02      -39.558684        0.069338
FIRE:  239 05:54:02      -39.558739        0.053432
FIRE:  240 05:54:02      -39.558807        0.061351
FIRE:  241 05:54:02      -39.558888        0.048277

もしログを抑制したい場合は、FIRE(neb, logfile=None)のような指定をするとデフォルトのoptのログが表示されなくなります。

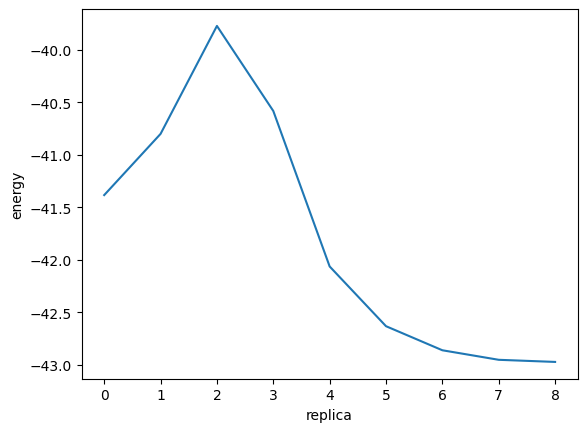
結果を見てみましょう。以下はmatplotlibを用いてエネルギーの軌跡を可視化したものです。

エネルギーが一度上がった後で下がる反応が見えていると思います。このエネルギーが最大の点(遷移状態、transition state)と左右の安定点それぞれとのエネルギー差が活性化エネルギーに相当します。

[7]:

energies = np.array([image.get_total_energy() for image in images])

fig = plt.figure()
ax = fig.add_subplot(1, 1, 1)
ax.plot(energies)
ax.set_xlabel("replica")
ax.set_ylabel("energy")
fig.show()

活性化エネルギーは以下のように計算できます。

ここでは、順反応X→Yにおける活性化エネルギーを E_act_forward、逆反応Y→Xにおける活性化エネルギーを E_act_backwardとしています。

[8]:

# Transition state takes maximum energy in the reaction path
ts_index = np.argmax(energies)

E_act_forward = energies[ts_index] - energies[0]
E_act_backward = energies[ts_index] - energies[-1]

print(f"ts_index       = {ts_index}")
print(f"E_act_forward  = {E_act_forward:.2f} eV")
print(f"E_act_backward = {E_act_backward:.2f} eV")

ts_index       = 3
E_act_forward  = 1.93 eV
E_act_backward = 3.48 eV

結果を見てみましょう。構造についても同様にNotebookに可視化してもいいですが、画像をファイルとして保存することもできます。今回は試しにそちらを実行してみましょう。

今回はNEBのため、結果は構造1つではなく一組の軌跡として出力されています。ASEからアニメーションGIFとして保存してみましょう。

[9]:

fig = plt.figure(facecolor="white")
ax = fig.add_subplot()
ase.io.write(
    "output/curtius_NEB.gif",
    images,
    format="gif",
    ax=ax
)

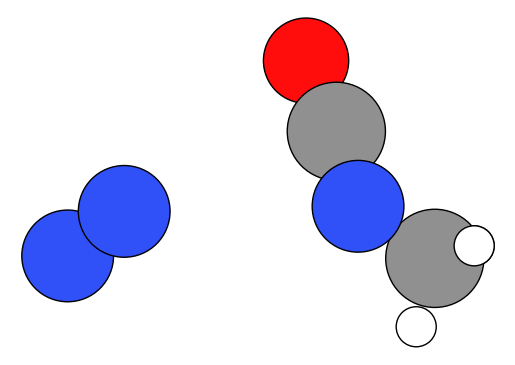
上には最終構造の静止画が表示されていると思いますが、左のファイルビューアから”curtius_NEB.gif”をダブルクリックして開くと直接アニメーションGIFを見ることができます。

以下のようにしてファイルの中身を表示することができます。

[10]:

Image("output/curtius_NEB.gif", format="gif")

[10]:

<IPython.core.display.Image object>

最後に追加で、NEB法により反応経路の最適化前後がどう変わったのかを比較してみましょう。

neb.interpolate()関数を呼び、FIRE optを行う前の反応経路の候補構造 interpolated_images とNEB法で最適化された後の images のエネルギーを比べてみます。

[11]:

_images = [react.copy()]
_images += [react.copy() for i in range (7)]
_images += [prod.copy()]
for image in _images:
    estimator = Estimator()
    calculator = ASECalculator(estimator)
    image.calc = calculator
neb = NEB(_images, k=0.1, climb=True, allow_shared_calculator=False, parallel=True)
neb.interpolate()
interpolated_images = _images

/tmp/ipykernel_38727/4187733795.py:8: FutureWarning: Please import NEB from ase.mep, not ase.neb.
  neb = NEB(_images, k=0.1, climb=True, allow_shared_calculator=False, parallel=True)

[12]:

initial_energies = [image.get_total_energy() for image in interpolated_images]
opt_energies = [image.get_total_energy() for image in images]

fig = plt.figure()
ax = fig.add_subplot(1, 1, 1)
ax.plot(initial_energies, label="neb interpolated", color="red")
ax.plot(energies, label="after neb opt")
ax.set_xlabel("replica")
ax.set_ylabel("energy")
ax.legend()
fig.show()

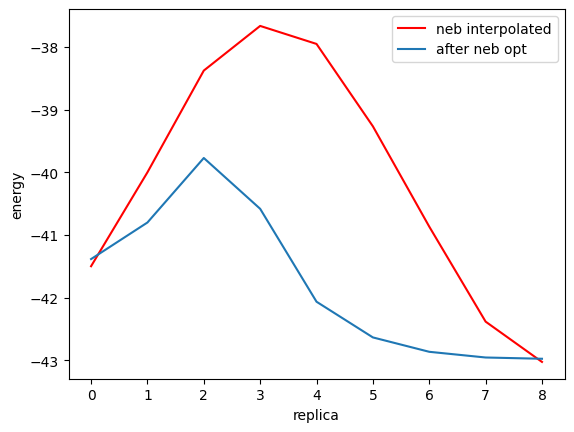
上記図からもわかるように、NEBの反応経路探索により、反応経路の候補構造(赤線)よりも活性化エネルギーエネルギーが低くなる経路=遷移状態のエネルギーが低い経路(青線) が見つかったことがわかります。

[コラム] 反応経路解析手法と分子動力学法の比較¶

本節では、反応を見るために始状態・終状態を指定したNEB法により反応経路の探索を行いました。

次章で説明するような分子動力学法では、原子の時間発展を追うことができますが、そのような形でシミュレーションを行い自然と反応が起きるまで待つというアプローチはどうでしょうか？この方法でも活性化エネルギーの解析ができる例はあり、以下のLi ionの拡散現象はそのような例となります。

硫化物固体電解質中のLi拡散 | MATLANTIS

しかし、一般的には反応時間が課題となります。反応というのはレアイベントです。アレニウスの式を見ても分かる通り、活性化エネルギー \(E_a\) に対して指数関数的に発生頻度が変わる現象です。

\[k = A \exp \left(- \frac{E_a}{k_B T} \right)\]

そのため、活性化エネルギーがとても低い場合はMDでもその反応を見ることができますが、すこしでも高くなってくると、MDで扱える時間スケール (〜ns程度)ではその反応が起きず、効率的に見つけることはできません。さらに活性化エネルギーが高くなれば日常の世界でもおこらないような現象となります。

参考までに、具体的な値を通して活性化エネルギーと現象の起こりやすさの関係を見てみましょう。ほぼ室温である300 Kでは、アレニウスの式の指数関数内部の分母にあたる\(k_B T\)の値はおおまかに0.026 eVとなります。これは、エネルギーが1 eV高い現象の起きやすさが\(\exp\left(-1/0.026\right)\)倍、つまり\(2\times10^{-17}\)倍に下がるということを意味します。これはマクロスケールと原子スケールの差を考慮してもなお大きな値であり、レアイベントとみなすことができます。同様に計算すると、温度が1000 Kおよび2000 Kの場合は\(k_B T\)はそれぞれ0.086 eV, 0.172 eVとなり、エネルギーが1 eV高い現象の起きやすさはそれぞれ約\(9\times10^{-6}\)倍、 \(0.003\)倍となります。これは300 Kのときの値と比べると大幅に大きくなっており、マクロスケールでは頻繁に起きる現象とみなすことができます。このように、一般に現象の起きやすさは活性化エネルギーと温度に対して非常に鋭敏に変化するものであることが知られています。 NEB法のような反応経路解析を使うことによって、このような指数関数スケールにまたがるレアイベントを効率的に分析することが可能となります。

[13]:

from ase.units import kB
from math import exp

for T in [300, 1000, 2000]:
    kBT = kB * T
    ratio = exp(-1 / (kBT))

    print(f"----- T = {T} K -----")
    print(f"kB T : {kBT:.3f}")
    print(f"ratio: {ratio:.2e}")

----- T = 300 K -----
kB T : 0.026
ratio: 1.59e-17
----- T = 1000 K -----
kB T : 0.086
ratio: 9.12e-06
----- T = 2000 K -----
kB T : 0.172
ratio: 3.02e-03

このように、MDではみることが難しいような反応も、NEB法などを使うことで効率的に探索することができる可能性があります。

この他、反応経路探索に関するいくつかのアプローチ方法を以下に記載します。

アプローチ	特徴	手法例
特定の反応経路を対象とする反応経路探索	ある2つの安定構造をつなぐ経路を出発点として、近傍の最小エネルギー経路(MEP: Minimum Energy Path)を求める手法。比較的少ない計算コストでMEPおよび対応する遷移状態を見つけられるが、いわゆる局所探索のため、結果は探索前に想定した反応経路に強く依存する。	NEB法・String法など
反応経路を事前に想定しない反応経路探索	反応経路や反応後の構造を事前に仮定せずに、反応経路を1つ以上見つける方法。標準的なMDを行う方法以外に、効率的にエネルギー曲面を探索することを目的としたメタダイナミクス、局所的なエネルギー曲面の情報を使って探索する手法(ADDF)などがある。	MD、メタダイナミクス、ADDFなど

参考文献¶

反応経路探索手法についてさらに知りたい方は、以下の文献も参考になるでしょう。