ASE Calculator¶

前節では、ASEのAtomsについての基礎や構造生成方法について学びました。

本節では、物理シミュレーションを行う上で必要となる Calculator の取り扱い方を学びます。

https://wiki.fysik.dtu.dk/ase/ase/calculators/calculators.html

エネルギー(Energy)¶

系の全エネルギー $E$ (Total energy) は、運動エネルギー $K$ (Kinetic energy)と、ポテンシャルエネルギー $V$ (Potential energy)で表されます。

\[E = K + V\]

このうち、原子の運動エネルギー$K$は古典力学の表式を用い以下のように計算できます。

\[K = \sum_{i=1}^{N} \frac{1}{2} m_i {\mathbf{v}}_i^2 = \sum_{i=1}^{N} \frac{{\mathbf{p}}_i^2}{2 m_i}\]

ここで $m_i, \mathbf{v}_i, \mathbf{p}_i$ はそれぞれ各原子の質量 (mass) 、速度 (velocity)および運動量 (momenta, $\mathbf{p}=m\mathbf{v}$)です。

(太字で表されているものはベクトルを表しています、ここでの速度:math:mathbf{v}や運動量$\mathbf{p}$はxyz座標の３成分を持っています。)

一方で、ポテンシャルエネルギー$V$は、厳密に求めるためには量子力学から導かれる方程式（Schrodinger方程式など、コラム参照)を解く必要があり簡単ではありません。ポテンシャルエネルギーを求める方法として、高速に計算可能だが適応可能領域に制限のある古典力場から、計算時間はかかるが精度の良いDFT(密度汎関数法)などの量子化学計算を用いる方法まで様々な方法が存在します。（これらの違いは後述します。）

では、なぜそもそもエネルギーを知りたいのでしょうか？逆にいうと、エネルギーからどういったことがわかるのでしょうか？代表的なこととして、

１つめに、ある物質の安定構造を知ることができます。２章でも説明を行うように、自然界で物質がどのような３次元構造をとり安定しているかは自明ではありません。エネルギーが低いか高いかなどをみることで、自然界でその構造が実現するかどうかといった解析を行うことができます。

2つめに、物質の各原子がどのように動くのかを知ることができます。次節で説明します。

力(force)¶

古典力学で、ニュートンの運動方程式は以下のように表されます。

\[\mathbf{F} = m\mathbf{a}\]

この式が表すことは、力(force) $\mathbf{F}$が与えられると、その系に加わる加速度 $\mathbf{a}$ がわかるというものです。各原子の位置$\mathbf{r}$、速度$\mathbf{v}$、加速度$\mathbf{a}$は、以下のような関係です。

\[\mathbf{v} = \frac{d\mathbf{r}}{dt}\]

\[\mathbf{a} = \frac{d\mathbf{v}}{dt} = \frac{d^2\mathbf{r}}{dt^2}\]

つまり力がわかると、加速度(=速度がどうかわるか)がわかり、結果位置がどのように時間発展するのかも知ることができます。 ※実際にこの方法で時間発展を扱うMD (分子動力学法)は6章で扱います。

この力は、ポテンシャルエネルギーの位置微分で表すことができます。

\[\mathbf{F} = -\frac{\partial V}{\partial \mathbf{r}}\]

まとめると、系の時間発展$\mathbf{r}(t)$を知るために必要な力$\mathbf{F}$の情報は、ポテンシャルエネルギー$V\mathbf(r)$がわかれば計算できる。ということになります。

[Note] 本チュートリアルでは、簡単のため、古典力学の知識のみで説明を行いました。解析力学を習ったことのある方向けの言葉で説明をすると、ハミルトニアンにより支配方程式が規定されるため、ハミルトニアン(上述のエネルギーに関連する関数)を知ることで系の時間発展を記述することができます。

Calculatorクラスとは？¶

ここまでで、ポテンシャルエネルギー$V(\mathbf{r})$が決まれば、物質の支配方程式、すなわちこの世界でどのように物質が動くのか、がわかることを説明しました。

ASEではポテンシャルエネルギーの計算をCalculatorクラスが担当し、Calculatorを切り替えることによってその計算方法を切り替えることができます。

１つ例を見てみましょう。以下はH2 の各エネルギーをMatlantisが提供するPFPのCalculatorを用いて計算しています。

詳細な使い方は後述しますが、atoms.calcにたいしてCalculatorをセットすることで各種エネルギーの計算ができるようになります。ここでは、

全エネルギー $E$: atoms.get_total_energy()
ポテンシャルエネルギー $V$: atoms.get_potential_energy()
運動エネルギー $K$: atoms.get_kinetic_energy()

を計算しています。

[1]:

from ase import Atoms

import pfp_api_client
from pfp_api_client.pfp.calculators.ase_calculator import ASECalculator
from pfp_api_client.pfp.estimator import Estimator, EstimatorCalcMode


# print(f"pfp_api_client: {pfp_api_client.__version__}")

estimator = Estimator()
calculator = ASECalculator(estimator)

[2]:

atoms = Atoms("H2", [[0, 0, 0], [1.0, 0, 0]])
atoms.set_momenta([[0.1, 0, 0], [-0.1, 0, 0]])
atoms.calc = calculator

E_tot = atoms.get_total_energy()
E_pot = atoms.get_potential_energy()
E_kin = atoms.get_kinetic_energy()

print(f"Total Energy     : {E_tot:f} eV")
print(f"Kinetic Energy   : {E_kin:f} eV")
print(f"Potential Energy : {E_pot:f} eV")

Total Energy     : -3.808640 eV
Kinetic Energy   : 0.009921 eV
Potential Energy : -3.818561 eV

Atomsははじめは初速度0で、運動エネルギーが0 となるため、適当な初速度を set_momenta 関数を用いて設定しました。

$ E = K + V $ になっているのが確認できます。

全エネルギー $E$やポテンシャルエネルギー$V$ の計算で Calculatorが必要で、atoms.calc = calculator の設定がないと計算ができずエラーとなります。

Calculatorの種類¶

ASEでは、古典力場から量子化学計算を用いたCalculatorまで様々なものがサポートされていますが、以下にいくつか例を上げてみます。

ここに示した以外にも多くのCalculatorがサポートされています。詳しくは Supported calculators をご確認ください。

カテゴリー	Calculator	ASE組み込み	説明
古典力場	lj	✓	Lennard-Jones potential
	morse	✓	Morse potential
	emt	✓	Effective Medium Theory calculator
	lammps		Classical molecular dynamics code
量子化学計算	gaussian		Gaussian based electronic structure code
	vasp		Plane-wave PAW code
	espresso		Plane-wave pseudopotential code
NNP (Neural Network Potential)	PFP		Matlantisの提供するポテンシャル

上記で、“ASE組み込み”に✓のついているものは、ASEをインストールするだけで使用することが可能となりますが、それ以外のCalculatorは外部プログラムをインストールして連携する必要があります。

量子化学計算を行うタイプのCalculatorは、量子力学から導出されるSchrodinger方程式をある一定の近似のもとで解くことで理論的にポテンシャルを計算します(以下のコラムも参照)。専用のソフトウェアが必要であり計算に時間がかかるものもあります。より精度の高い計算を行いたいときに使用します。

古典力場に属するタイプのLennard-Jones potential, Morse potentialなどは、人手で作成した(経験的な)関数系を用いてポテンシャルを計算する方法です。計算速度は早いですが、それぞれの手法ごとに対応できる構造や物理現象が異なり、確認が必要です。

NNPタイプは、事前にたくさんの量子化学計算などで計算したデータを用意し、入力構造とそのポテンシャルエネルギーの関係を教師あり学習させることにより、高速な計算時間で高精度なポテンシャル予測を行うことを目指しています。 NNPについて、詳しくは以下のスライドなども参考にしてください。

PFP：材料探索のための汎用Neural Network Potential - 2021/10/4 QCMSR + DLAP共催

ASE組み込みCalculator¶

ここではEMT Calculatorを使用してみます。

[3]:

from ase.build import bulk
from ase.calculators.emt import EMT


calculator_emt = EMT()

atoms = bulk("Cu")
atoms.calc = calculator_emt

E_pot_emt = atoms.get_potential_energy()
print(f"Potential energy {E_pot_emt:.5f} eV")

Potential energy -0.00568 eV

このようにCalculatorを切り替えて原子シミュレーションを行うことができます。

厳密なポテンシャルエネルギー$V(\mathbf{r})$を高速に計算することができれば、Calculatorを切り替える必要はなく常にそれを用いてシミュレーションを行えば良いのですが、現実では厳密なポテンシャルエネルギーを計算することはできず、その正確さと速度にはトレードオフの関係が存在します。そのため、原子シミュレーションを行うユーザーが用途に合わせて選択を行う必要があります。

PFP¶

Matlantisの提供するPFPは 汎用・高速で有ることを特徴としており、55元素の組み合わせで様々な構造の系に対して高速に計算を行うことが可能です。本チュートリアルでは、全体を通して主にPFPのCalculatorを使用します。

[4]:

import pfp_api_client
from pfp_api_client.pfp.calculators.ase_calculator import ASECalculator
from pfp_api_client.pfp.estimator import Estimator, EstimatorCalcMode

estimator = Estimator(model_version="v2.0.0")
calculator = ASECalculator(estimator)

atoms.calc = calculator

E_pot_emt = atoms.get_potential_energy()
print(f"Potential energy {E_pot_emt:.5f} eV")

Potential energy -3.07547 eV

上記EMTとPFPではエネルギーの絶対値が大きく違っていますが、系のエネルギーを定義する際にその絶対値はシフトする任意性があります。

同じ原子数からなる２つの異なる系のエネルギーの差には意味がありますが、それぞれの絶対値にはあまり意味がないので注意してください。

AtomsとCalculatorの関係¶

ASEライブラリでは、原子構造をAtomsクラスで表し、そこにCalculatorをセットすることでそのAtomsに関する各基本物性値（エネルギー・力・ストレス・電荷など）を計算することができます。 Calculatorをセットする際には atoms.calc に対して直接 calculatorをセットします。

Atoms と Calculatorの関係

b33b3c15b0304d7d9b345b8903fcac27

Calculatorを経由して計算できる基本物性値と、その計算methodは以下のようになっています。

ポテンシャルエネルギー: get_potential_energy
力: get_forces
応力(ストレス): get_stress
電荷: get_charges
磁気モーメント: get_magnetic_moment
双極子モーメント: get_dipole_moment

[5]:

calculator = ASECalculator(Estimator())

atoms = bulk("Pt") * (2, 2, 1)
atoms.calc = calculator

E_pot = atoms.get_potential_energy()
charges = atoms.get_charges()
forces = atoms.get_forces()
stress = atoms.get_stress()

print(f"E_pot {E_pot:.2} eV")
print(f"charges {charges} C")
print(f"forces {forces} eV/A")
print(f"stress {stress} eV/A^2")

E_pot -2.2e+01 eV
charges [ 1.56390826e-07  4.79747513e-08  1.49468789e-07 -3.53834395e-07] C
forces [[ 1.21045008e-06 -1.28531060e-07  1.16374716e-06]
 [-8.99028036e-07  9.10295516e-07 -7.65895014e-07]
 [ 8.04090586e-07 -1.76741016e-06  1.52298933e-06]
 [-1.11551263e-06  9.85645703e-07 -1.92084147e-06]] eV/A
stress [-5.98167504e-02 -5.98167416e-02 -5.98167977e-02  9.46340221e-09
 -2.35475377e-08 -5.36077254e-09] eV/A^2

PFP では、 magnetic momentや dipole moment の計算には対応していません。 (magnetic momentは電子状態を表すもので、本チュートリアルのスコープであるAtomistic simulationでは使いません。)

[6]:

# Some Calculator supports this, but PFP calculator raises error.

# magmom = atoms.get_magnetic_moment()
# dipole = atoms.get_dipole_moment()

以下の[コラム]はアドバンストな内容を含みます、Tutorialを読み進めていく上ではスキップも可能です。

[コラム] Calcultor の計算キャッシュ機能¶

Calculatorは前に計算を行った際の入力原子構造を calculator.atomsに、　またそのときの計算結果を calculator.results に保持しています。そのため、以前と全く同じ原子構造に対して物性値の get_XXX 関数を呼んだ場合、 再計算をスキップ するような仕組みになっています。

[7]:

atoms.calc = calculator
calculator.reset()

[8]:

%time Epot = atoms.get_potential_energy()
%time Epot = atoms.get_potential_energy()

CPU times: user 3.06 ms, sys: 0 ns, total: 3.06 ms
Wall time: 94 ms
CPU times: user 375 µs, sys: 61 µs, total: 436 µs
Wall time: 383 µs

上記の例でWall timeを比較すると、１回目の実行ではミリ秒オーダーの時間がかかっており計算が実行されていますが、２回めの実行では計算がスキップされているためミリ秒もかからずにエネルギーを得ることができていることがわかります。

calculator.reset() を呼ぶことで明示的に計算結果のキャッシュをクリアして再計算を行うこともできます。以下の例では2回めの計算でもミリ秒の計算時間がかかっていることがわかります。

[9]:

calculator.reset()

print("----- 1st calc -----")
%time Epot = atoms.get_potential_energy()

print(f"After 1st calc   : {calculator.results}")
calculator.reset()
print(f"After reset      : {calculator.results}")

print("----- 2nd calc -----")
%time Epot = atoms.get_potential_energy()
print(f"After 2nd calc   : {calculator.results}")

----- 1st calc -----
CPU times: user 3.16 ms, sys: 285 µs, total: 3.44 ms
Wall time: 90.3 ms
After 1st calc   : {'energy': -21.712707825955075, 'forces': array([[-1.78798193e-07,  8.57089841e-08, -9.71775560e-07],
       [-3.81674838e-07,  2.40788247e-07,  4.98792271e-07],
       [ 9.00971539e-07, -2.72842101e-07,  1.12511234e-06],
       [-3.40498508e-07, -5.36551305e-08, -6.52129048e-07]]), 'charges': array([-2.17493621e-07, -2.45786026e-07, -9.83995818e-09,  4.73119684e-07]), 'calc_stats': {'elapsed_usec_infer': 36693, 'elapsed_usec': 83022, 'elapsed_usec_preprocess': 3930, 'n_neighbors': 400}, 'free_energy': -21.712707825955075, 'stress': array([-5.98166255e-02, -5.98166500e-02, -5.98166300e-02,  4.26570321e-08,
       -4.45518682e-08,  3.79886465e-08])}
After reset      : {}
----- 2nd calc -----
CPU times: user 1.66 ms, sys: 0 ns, total: 1.66 ms
Wall time: 57.7 ms
After 2nd calc   : {'energy': -21.712705946017945, 'forces': array([[ 9.52835494e-08,  9.18911048e-07, -3.93850900e-07],
       [-7.98279949e-07, -4.07897529e-07,  1.47059723e-06],
       [-3.51072639e-07, -3.76604209e-07,  3.40857921e-07],
       [ 1.05406904e-06, -1.34409311e-07, -1.41760425e-06]]), 'charges': array([-2.72528879e-08, -3.71969477e-08, -1.25965400e-07,  1.90415335e-07]), 'calc_stats': {'n_neighbors': 400, 'elapsed_usec_infer': 46355, 'elapsed_usec': 51052, 'elapsed_usec_preprocess': 3135}, 'free_energy': -21.712705946017945, 'stress': array([-5.98171226e-02, -5.98171468e-02, -5.98171011e-02,  1.97083025e-08,
       -1.43127693e-08,  1.31512884e-08])}

なお、原子構造が少しでも変わった場合には calculator.resultの結果を破棄し、新しく計算がされます。

以下の例では、水素分子の原子間距離を変えて再度 atoms.get_potential_energyを呼んでいますが、この場合は入力原子構造が変わったことを Calculator が検知して新しく計算を行います。実際にどちらの計算にもミリ秒オーダーのWall timeがかかっていることがわかります。

[10]:

atoms = Atoms(["H", "H"], positions=[[0, 0, 0], [0, 0, 0.8]])

atoms.calc = calculator
%time E_pot1 = atoms.get_potential_energy()
# --- calculator.atoms stores the previously calculated atoms
# print(calculator.atoms.positions)

# Change atomic distance to 2A
atoms.positions[1, 2] = 2.0
# --- The preveously calculated `calculator.atoms` and current calculate target `atoms` are
# different, so calculation is executed.
%time E_pot2 = atoms.get_potential_energy()
# print(calculator.atoms.positions)

print(f"E_pot1 {E_pot1:.2f} eV")
print(f"E_pot2 {E_pot2:.2f} eV")

CPU times: user 3.2 ms, sys: 0 ns, total: 3.2 ms
Wall time: 54 ms
CPU times: user 2.52 ms, sys: 0 ns, total: 2.52 ms
Wall time: 54.1 ms
E_pot1 -4.48 eV
E_pot2 -0.31 eV

[コラム] PFP Calculatorについて¶

※本節はMatlantis固有の挙動の解説です。

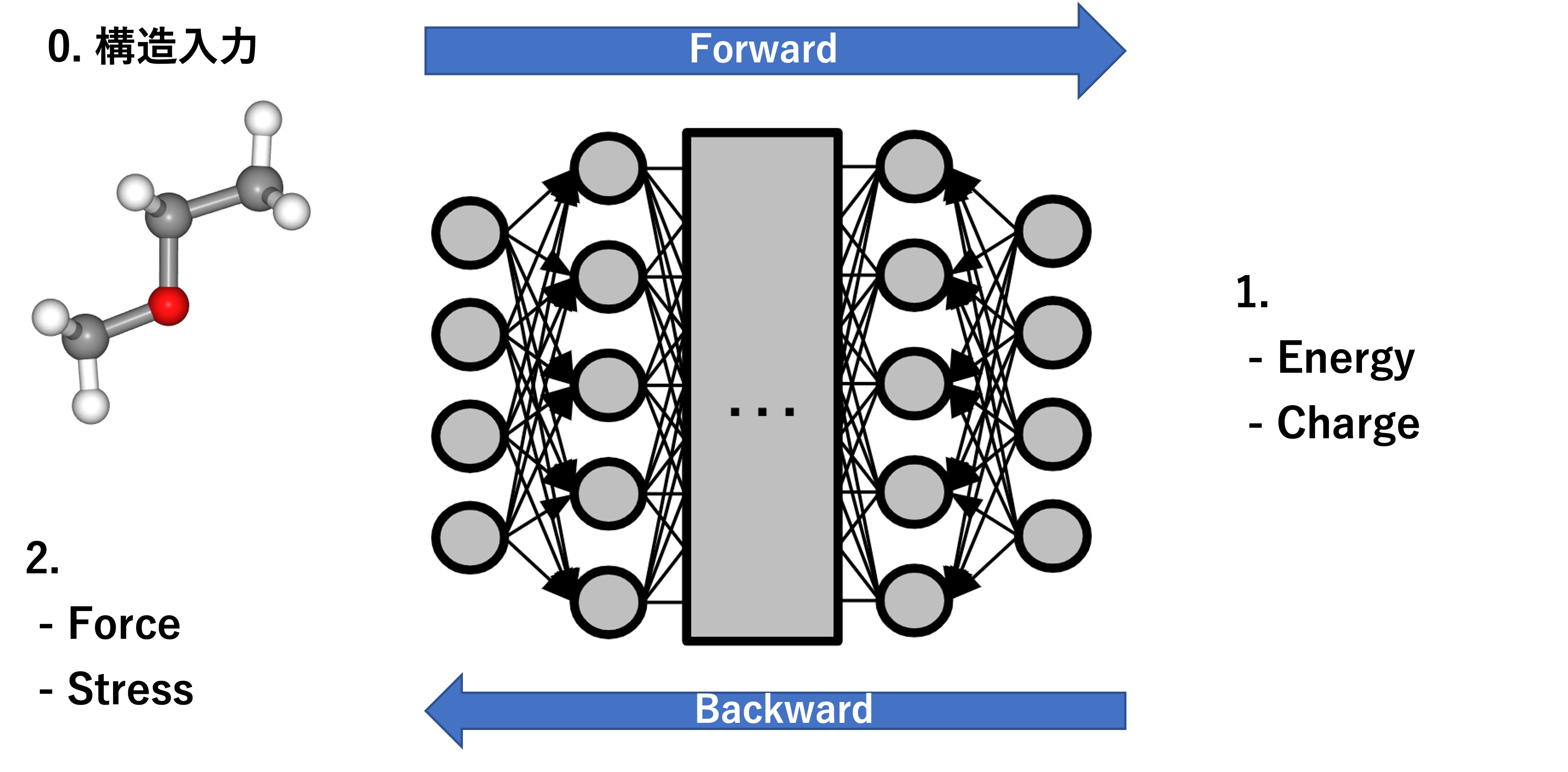
pfp-api-clientライブラリが提供しているASECalculatorの動作に関する説明を行います。

PFPでは potential_energy, charge がNNPのForwardで、forces, stress がNNPのBackwardで計算されるという挙動になっています。

04e548f29c564bf29c9e511017385306

[コラム] 量子化学計算で求めているポテンシャルエネルギーについて¶

冒頭の全エネルギーの説明では、運動エネルギーの表式は出てきましたが、ポテンシャルエネルギーについては表式が出てきておらずCalculatorが計算するものというだけの説明でした。このポテンシャルエネルギーは理論的にはどのように表されるのでしょうか。

原子レベルのミクロなスケールで起こる現象をシミュレーションしたい場合、その電子状態まで考慮してエネルギーなどを求めるには量子力学の理論が必要となります。定常状態の場合、以下で与えられるSchrödinger 方程式によって、系全体の状態を表す波動関数 $\Phi$、全エネルギー $E$が求まります。

\[\mathcal{H} | \Phi \rangle = E | \Phi \rangle\]

非相対論に基づき、原子核がM個と電子がN個からなる系を考えた場合のハミルトニアン $\mathcal{H}$は、原子単位系で以下のようにかけます。

\[\mathcal{H} = - \sum_{i=1}^N \frac{1}{2} \nabla^2_i - \sum_{A=1}^M \frac{1}{2 M_A} \nabla^2_A - \sum_{i=1}^N \sum_{A=1}^M \frac{Z_A}{r_{iA}} + \sum_{i=1}^N \sum_{j>i}^N \frac{1}{r_{ij}} + \sum_{A=1}^M \sum_{B>A}^M \frac{Z_A Z_B}{R_{AB}}\]

$M_A$: 原子核 $A$ の質量
$R_{AB}$: 原子核 $A$ と原子核 $B$ の距離
$r_{Ai}$: 原子核　$A$ と電子 $i$ の距離
$r_{ij}$: 電子 $i$ と電子 $j$ の距離
$Z_A$: 原子核$A$ の原子番号 = 陽子の数

であり、電子はすべて電荷 -1 です。

１項目は電子の運動エネルギー、2項目は原子核の運動エネルギー、3項目は電子と原子核の静電相互作用エネルギー、４項目は電子同士の静電相互作用エネルギー、5項目は原子核同士の静電相互作用エネルギーに対応しています。

これをこのまま解くのは難しいため、 Born-Oppenheimer 近似 を行うことが慣例となります。電子は原子核に比べてとても軽いため、原子核よりも早く動きます。そのため、原子は完全に静止しているとして、その時の電子の定常状態を求めるというものです。

そうするとN個の電子に対するSchrödinger方程式は

\[\mathcal{H}_{\rm{elec}} = - \sum_{i=1}^N \frac{1}{2} \nabla^2_i - \sum_{i=1}^N \sum_{A=1}^M \frac{Z_A}{r_{iA}} + \sum_{i=1}^N \sum_{j>i}^N \frac{1}{r_{ij}}\]

として、以下のようにかけます。

\[\mathcal{H}_{\rm{elec}} | \Phi_{\rm{elec}} \rangle = E_{\rm{elec}} | \Phi_{\rm{elec}} \rangle \tag{1}\]

原子核が静止しているときの全エネルギーは、

\[V = E_{\rm{elec}} + \sum_{A=1}^M \sum_{B>A}^M \frac{Z_A Z_B}{R_{AB}}\]

とかけます。これが、ポテンシャルエネルギーと対応付けられます。

これを解くことができれば、古典力場のようにパラメータを導入することなく、量子力学という基本法則のみからポテンシャルエネルギーを得ることができるはずです。「基礎物理定数以外の実験値に依存しない量子力学に基づいた計算手法」は第一原理計算 (first-principles calculation, ab initio calculation)と呼ばれます。

現実問題としては、この電子系に対するSchrödinger方程式 (1) は厳密に解くことはできないことが知られており、手法により様々な近似・仮定を置くことで解いています。 Hartree-Fock法、DFT(密度汎関数法)などがその代表例です。

ということで、ASEの扱うポテンシャルエネルギー $V$ というのは、電子・原子核の静電potential+電子の運動エネルギーを含む値になっていて、運動エネルギー $K$は原子核のみの運動エネルギーと捉えることができます。

[参考文献]

“MODERN QUANTUM CHEMISTRY Introduction to Advanced Electronic Structure Theory”, Attila Szabo and Neil S. Ostlund