[Advanced] 対称性を考慮した構造最適化¶
前節で基本的な事例に対する構造最適化を学びました。 本節はより発展的な内容として、系の対称性を保ちながら構造最適化を行う方法について学びます。
ASEでは空間群 (spacegroup)を扱う機能があり、 FixSymmetry というConstraintsクラスを利用することで対称性を考慮した構造最適化が行なえます。
本節は発展的な位置付けとします。次節へ急ぎたい方はスキップし、後から読んでいただいても構いません。
BaTiO\(_3\) の構造最適化¶
空間群や本節でいう“対称性”とは何なのかの詳細説明の前に、具体例を見ていきます。
ここではペロブスカイト構造をもつ物質として知られる、BaTiO\(_3\)(チタン酸バリウム)の構造最適化を考えてみます。
BaTiO\(_3\)は高い比誘電率を持つことからセラミック積層コンデンサなどの誘電体材料として使用されている人工鉱物で、室温では正方晶 (tetragonal)の構造をとっています。詳しくは、以下のページが参考になります。
構造ファイルはMaterials Projectより取得しています。
以下の正方晶(tetragonal)構造を持つBaTiO\(_3\)のセルは、\(a = b \neq c\), \(\alpha = \beta = \gamma =\) 90°となっています。(\(a = b = c\), \(\alpha = \beta = \gamma =\) 90°の場合は立方晶 (cubic)となります。)
[1]:
from ase.io import read
from pfcc_extras.visualize.view import view_ngl
bto_tetra = read("../input/BaTiO3_mp-5986_computed.cif")
print(f"BaTiO3 (Tetragonal): cell = {bto_tetra.cell.cellpar()}")
view_ngl(bto_tetra, representations=[])
BaTiO3 (Tetragonal): cell = [ 4.004457 4.004457 4.200636 90. 90. 90. ]
[2]:
view_ngl(bto_tetra * (4, 4, 4), representations=[])
get_scaled_positions関数を用いると、各原子の絶対座標ではなく、ユニットセルにおける相対座標を得ることができます。(つまり、[0, 0, 0]を原点、[1, 1, 1] がユニットセルの逆端の点となるような座標スケールです。)
今回の構造でscaled_positionsを確認してみると、xy座標に関しては 0や0.5 といったきりの良い数字をとっていることがわかります。
[3]:
bto_tetra.get_scaled_positions()
[3]:
array([[0.5 , 0.5 , 0.004136],
[0. , 0. , 0.524313],
[0. , 0.5 , 0.479349],
[0.5 , 0. , 0.479349],
[0. , 0. , 0.958854]])
この構造に対して、
本節で説明する、
FixSymmetryを用いる・用いない場合前節で説明済みの
ExpCellFilterのhydrostatic_strainがTrue,Falseの場合
の以下4通りの方法で構造最適化してみましょう。
[4]:
import pfp_api_client
from pfp_api_client.pfp.calculators.ase_calculator import ASECalculator
from pfp_api_client.pfp.estimator import Estimator, EstimatorCalcMode
estimator = Estimator(calc_mode=EstimatorCalcMode.CRYSTAL, model_version="v3.0.0")
calculator = ASECalculator(estimator)
構造最適化前のポテンシャルエネルギー
[5]:
bto_tetra.calc = calculator
Epot = bto_tetra.get_potential_energy()
print(f"Epot before opt: {Epot} eV")
Epot before opt: -31.54281016948673 eV
[6]:
from ase import Atoms
from ase.calculators.calculator import Calculator
from ase.constraints import ExpCellFilter
from ase.optimize import FIRE
from ase.constraints import FixSymmetry
def opt_with_symmetry(
atoms_in: Atoms,
calculator: Calculator,
fix_symmetry: bool = False,
hydrostatic_strain: bool = False,
) -> Atoms:
atoms = atoms_in.copy()
atoms.calc = calculator
if fix_symmetry:
atoms.set_constraint([FixSymmetry(atoms)])
ecf = ExpCellFilter(atoms, hydrostatic_strain=hydrostatic_strain)
opt = FIRE(ecf, logfile=None)
opt.run(fmax=0.005)
cell_diff = (atoms.cell.cellpar() / atoms_in.cell.cellpar() - 1.0) * 100
print("Optimized Cell :", atoms.cell.cellpar())
print("Optimized Cell diff (%):", cell_diff)
print("Scaled positions :\n", atoms.get_scaled_positions())
print(f"Epot after opt: {atoms.get_potential_energy()} eV")
return atoms
1. FixSymmetryなし, hydrostatic_strain=False¶
結晶軸のa, b, c, \(\alpha, \beta, \gamma\) が全て独立に最適化されるため、ごく僅かではありますが角度が90°からずれるなど、正方晶の対称性が崩れてしまっていることがわかります。原子座標も自由に動いています。
[7]:
atoms1 = opt_with_symmetry(bto_tetra, calculator, fix_symmetry=False, hydrostatic_strain=False)
/tmp/ipykernel_1750/819195949.py:18: FutureWarning: Import ExpCellFilter from ase.filters
ecf = ExpCellFilter(atoms, hydrostatic_strain=hydrostatic_strain)
Optimized Cell : [ 3.999351 3.99935081 4.22621354 89.99999973 89.99999776 89.99999744]
Optimized Cell diff (%): [-1.27507905e-01 -1.27512654e-01 6.08896886e-01 -3.02345160e-07
-2.49438050e-06 -2.84332935e-06]
Scaled positions :
[[5.00000016e-01 5.00000010e-01 8.53036289e-03]
[1.59435257e-07 7.06001742e-08 5.26177155e-01]
[9.99999949e-01 4.99999954e-01 4.77548623e-01]
[4.99999884e-01 9.99999975e-01 4.77548659e-01]
[9.99999992e-01 9.99999991e-01 9.56196200e-01]]
Epot after opt: -31.543516660199565 eV
2. FixSymmetryあり, hydrostatic_strain=False¶
正方晶(tetragonal)構造の持つ対称性である、\(a = b \neq c\), \(\alpha = \beta = \gamma =\) 90°を保ちつつきちんと最適化ができており、今回の構造最適化における所望の結果が得られることがわかります。
また、xy座標のscaled_positionsも0や0.5 といったきりの良い数字を(ものすごく小さな数値誤差を除いて)保っていることがわかります。 ※ これは後述する P 4 m m という対称性に課されるサイト間の関係を保っているということになります。
[8]:
atoms2 = opt_with_symmetry(bto_tetra, calculator, fix_symmetry=True, hydrostatic_strain=False)
/home/jovyan/.py39/lib/python3.9/site-packages/spglib/spglib.py:115: DeprecationWarning: dict interface (SpglibDataset['std_lattice']) is deprecated.Use attribute interface ({self.__class__.__name__}.{key}) instead
warnings.warn(
/home/jovyan/.py39/lib/python3.9/site-packages/spglib/spglib.py:115: DeprecationWarning: dict interface (SpglibDataset['transformation_matrix']) is deprecated.Use attribute interface ({self.__class__.__name__}.{key}) instead
warnings.warn(
/home/jovyan/.py39/lib/python3.9/site-packages/spglib/spglib.py:115: DeprecationWarning: dict interface (SpglibDataset['std_rotation_matrix']) is deprecated.Use attribute interface ({self.__class__.__name__}.{key}) instead
warnings.warn(
/home/jovyan/.py39/lib/python3.9/site-packages/spglib/spglib.py:115: DeprecationWarning: dict interface (SpglibDataset['std_positions']) is deprecated.Use attribute interface ({self.__class__.__name__}.{key}) instead
warnings.warn(
/home/jovyan/.py39/lib/python3.9/site-packages/spglib/spglib.py:115: DeprecationWarning: dict interface (SpglibDataset['mapping_to_primitive']) is deprecated.Use attribute interface ({self.__class__.__name__}.{key}) instead
warnings.warn(
/home/jovyan/.py39/lib/python3.9/site-packages/spglib/spglib.py:115: DeprecationWarning: dict interface (SpglibDataset['std_mapping_to_primitive']) is deprecated.Use attribute interface ({self.__class__.__name__}.{key}) instead
warnings.warn(
/home/jovyan/.py39/lib/python3.9/site-packages/spglib/spglib.py:115: DeprecationWarning: dict interface (SpglibDataset['rotations']) is deprecated.Use attribute interface ({self.__class__.__name__}.{key}) instead
warnings.warn(
/home/jovyan/.py39/lib/python3.9/site-packages/spglib/spglib.py:115: DeprecationWarning: dict interface (SpglibDataset['translations']) is deprecated.Use attribute interface ({self.__class__.__name__}.{key}) instead
warnings.warn(
/tmp/ipykernel_1750/819195949.py:18: FutureWarning: Import ExpCellFilter from ase.filters
ecf = ExpCellFilter(atoms, hydrostatic_strain=hydrostatic_strain)
Optimized Cell : [ 3.99935145 3.99935145 4.22621104 90. 90. 90. ]
Optimized Cell diff (%): [-0.12749674 -0.12749674 0.60883732 0. 0. 0. ]
Scaled positions :
[[5.00000000e-01 5.00000000e-01 8.53034739e-03]
[7.17464814e-43 3.00975353e-35 5.26176962e-01]
[0.00000000e+00 5.00000000e-01 4.77548635e-01]
[5.00000000e-01 0.00000000e+00 4.77548635e-01]
[0.00000000e+00 0.00000000e+00 9.56196419e-01]]
Epot after opt: -31.54352290834058 eV
3. FixSymmetryなし, hydrostatic_strain=True¶
hydrostatic_strain=Trueの場合、等方的に圧力がかかるよう補正をするので、格子長の比と格子角を維持して最適化されます。 Optimized Cell diff (%)の部分を見るとわかるように、角度が90°なまま最適化できていますが、a, b, c軸が全て同じ比率で最適化されてしまっています。 結果として、c軸方向に伸びる構造最適化が進まずに極小値まで落ちきれていない事がわかります。(1, 2と比べると Epotが大きい値で構造最適化が終了してしまっています。)
また、原子座標に関しては自由に動くため、xy座標のscaled_positionsが0や0.5 といったきりの良い数字から少し離れていることがわかります。
[9]:
atoms3 = opt_with_symmetry(bto_tetra, calculator, fix_symmetry=False, hydrostatic_strain=True)
/tmp/ipykernel_1750/819195949.py:18: FutureWarning: Import ExpCellFilter from ase.filters
ecf = ExpCellFilter(atoms, hydrostatic_strain=hydrostatic_strain)
Optimized Cell : [ 4.00530335 4.00530335 4.20152382 90. 90. 90. ]
Optimized Cell diff (%): [0.0211353 0.0211353 0.0211353 0. 0. 0. ]
Scaled positions :
[[5.00000029e-01 5.00000017e-01 7.01999267e-03]
[1.64765465e-07 1.84306503e-07 5.24653378e-01]
[9.99999961e-01 4.99999863e-01 4.78119753e-01]
[4.99999878e-01 9.99999952e-01 4.78119744e-01]
[9.99999968e-01 9.99999985e-01 9.58088133e-01]]
Epot after opt: -31.54333787703485 eV
4. FixSymmetryあり, hydrostatic_strain=True¶
セルに関しては3.と同様の結果となりました。hydrostatic_strain=Trueとして格子長の比と格子角を維持するということが、FixSymmetryで課される制約よりも厳しいものとなっています。
原子座標に関してはFixSymmetryの制約により、xy座標のscaled_positionsが0や0.5 といったきりの良い数字を保っています。
[10]:
atoms4 = opt_with_symmetry(bto_tetra, calculator, fix_symmetry=True, hydrostatic_strain=True)
/tmp/ipykernel_1750/819195949.py:18: FutureWarning: Import ExpCellFilter from ase.filters
ecf = ExpCellFilter(atoms, hydrostatic_strain=hydrostatic_strain)
Optimized Cell : [ 4.00530331 4.00530331 4.20152377 90. 90. 90. ]
Optimized Cell diff (%): [0.0211343 0.0211343 0.0211343 0. 0. 0. ]
Scaled positions :
[[5.00000000e-01 5.00000000e-01 7.01994807e-03]
[1.76563607e-42 0.00000000e+00 5.24653369e-01]
[2.79559044e-43 5.00000000e-01 4.78119771e-01]
[5.00000000e-01 0.00000000e+00 4.78119771e-01]
[3.36311631e-43 0.00000000e+00 9.58088142e-01]]
Epot after opt: -31.543327059394755 eV
まとめ¶
結果を表にまとめると以下のようになります。
方法 |
|
|
結果 |
|---|---|---|---|
1 |
対称性が考慮されないため、セルの角度などが微小変化してしまう。 |
||
2 |
✓ |
所望の結果が得られる。 正方晶という対称性を保ちながら、十分な構造最適化が行える。原子座標のサイトの関係もきちんと制約がかかる |
|
3 |
✓ |
a, b, c軸全てが同じ割合で最適化されてしまうため、c軸方向の構造最適化が十分に行えない。原子座標も自由に動いてしまう。 |
|
4 |
✓ |
✓ |
セルは3と同様。原子座標のサイトの関係は制約がかかる。 |
格子の対称性とは「格子ベクトル・等価であるサイトの関係」のことであり（a=b, α=β=γ=90°など）、FixSymmetryを用いることでこの対称性を保ちながら構造最適化を行えます。より正確には、初期構造が属する空間群を保つような変位のみで構造最適化が行われます。
以下では、対称性に関する定義、つまり空間群について説明します。
空間群 (spacegroup)¶
3次元の空間に周期境界条件をもって規則的に続く結晶構造が取ることのできるパターンは、全部で230種類となることが知られており、これを空間群といいます。 全ての結晶は230種類の空間群のなかのどれか１つに属することとなります。
空間群の230種のリストに関しては、例えば以下のサイトなどで確認することができます。
ASEでは、get_spacegroup関数を用いることでatomsの空間群を判定することができます。
[Note]
get_spacegroup関数内ではspglibというライブラリが内部で用いられています。 spglibは、ユニットセルや原子座標の情報から、その空間群を判定するライブラリです。
“
Spglib: a software library for crystal symmetry search”, Atsushi Togo and Isao Tanaka, https://arxiv.org/abs/1808.01590
今回のBaTiO3 tetragonal構造に対して、空間群の判定を行ってみましょう。
[11]:
from ase.spacegroup import get_spacegroup
sg = get_spacegroup(bto_tetra)
sg
[11]:
Spacegroup(99, setting=1)
ここで返ってきた Spacegroup クラスからは以下のような情報を得ることができます。
no: 空間群の番号symbol: 空間群のヘルマン・モーガン記号(Hermann-Mauguin)。(他の表現方法としてはシェーンフリース記号(Schoenflies)が知られています。)lattice: 格子タイプ。P単純格子,I体心,F面心など。scaled_primitive_cell: 規格化された単位胞reciprocal_cell: 逆格子
[12]:
type(sg)
[12]:
ase.spacegroup.spacegroup.Spacegroup
[13]:
print("no : ", sg.no)
print("symbol : ", sg.symbol)
print("lattice : ", sg.lattice)
print("scaled_primitive_cell: \n", sg.scaled_primitive_cell)
print("reciprocal_cell : \n", sg.reciprocal_cell)
no : 99
symbol : P 4 m m
lattice : P
scaled_primitive_cell:
[[1. 0. 0.]
[0. 1. 0.]
[0. 0. 1.]]
reciprocal_cell :
[[1 0 0]
[0 1 0]
[0 0 1]]
今回のBaTiO\(_3\)構造は、99番目の P 4 m m 空間群と判定されました。
空間群は並進移動・回転・鏡像反転などのうち、どのような操作に対してその結晶構造が変わらない変換となるかを規定しています。 空間群の記号の読み方などに関しては、それだけで１冊の本になるほどの内容なので、ここでは割愛します。 詳細を勉強したい方は末尾の参考文献などをご参照ください。
本tutorialでは、可視化をしながら空間群がどういうものなのか感覚的な説明を試みます。 P 4 m m は、4回回転対称性を持ち(z軸方向に90度回転させる変換に対して不変)、xz平面およびyz平面に対して鏡像反転対称性を持つ空間群となっています。
ある１つの原子配置に対して、この対称性から課される“等価なサイト”は、equivalent_lattice_pointsという関数で計算できます。 以下のように、適当な点 ([0.3, 0.1, 0.6])に対して等価なサイトを計算し、表示してみましょう。
[14]:
sites, kinds = sg.equivalent_sites([[0.3, 0.1, 0.6]])
print("sites", sites)
p4mm_atoms = Atoms(symbols="C8", scaled_positions=sites, cell=[5, 5, 5], pbc=True)
view_ngl(p4mm_atoms)
sites [[0.3 0.1 0.6]
[0.7 0.9 0.6]
[0.9 0.3 0.6]
[0.1 0.7 0.6]
[0.3 0.9 0.6]
[0.7 0.1 0.6]
[0.9 0.7 0.6]
[0.1 0.3 0.6]]
このように、[0.3, 0.1, 0.6]からz軸方向に90度回転して得られる点や、それらの点からxz平面/yz平面に対する鏡像反転を行って得られる点、合計8点が等価なサイトとして含まれることがわかります。
BaTiO\(_3\)の構造を再度見てみましょう。
[15]:
view_ngl(bto_tetra)
[16]:
from pfcc_extras.visualize.ase import view_ase_atoms
view_ase_atoms(bto_tetra, figsize=(4, 4), title="BaTiO3 tetragonal atoms", scale=100, rotation="0x,0y,0z")
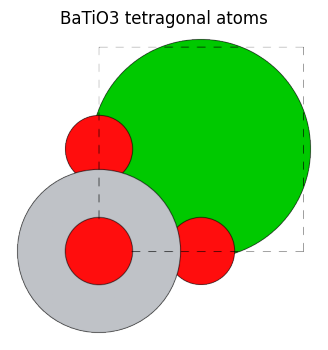
今回のBaTiO\(_3\)構造に関しては、 index=0のBa、index=1のTi、index=4のOに関しては、回転や鏡像反転を行ってもユニットセル分の移動を除いて同じ場所に移るため、等価なサイトは自分自身のみとなっています。 index2と3のO構造は4回回転対称性によりお互いに等価なサイトとなっていることがわかります。
[17]:
spos = bto_tetra.get_scaled_positions()
symbols = bto_tetra.symbols
for i in range(len(spos)):
print(i, symbols[i], sg.equivalent_sites(spos[i]))
0 Ba (array([[0.5 , 0.5 , 0.004136]]), [0])
1 Ti (array([[0. , 0. , 0.524313]]), [0])
2 O (array([[0. , 0.5 , 0.479349],
[0.5 , 0. , 0.479349]]), [0, 0])
3 O (array([[0.5 , 0. , 0.479349],
[0. , 0.5 , 0.479349]]), [0, 0])
4 O (array([[0. , 0. , 0.958854]]), [0])
最後に、本tutorial で構造最適化を行った後の4構造それぞれに対する空間群の判定をしてみます。
get_spacegroup関数のsymprec で対称性判定を行う際の各原子座標のずれの許容範囲を設定できます。 今回、defaultのsymprec=1e-5では全て P 4 m mとなってしまったため、厳しく小さな値を設定して空間群の判定を行っています。
[18]:
symprec = 1e-10
print("atoms1: ", get_spacegroup(atoms1, symprec=symprec).symbol)
print("atoms2: ", get_spacegroup(atoms2, symprec=symprec).symbol)
print("atoms3: ", get_spacegroup(atoms3, symprec=symprec).symbol)
print("atoms4: ", get_spacegroup(atoms4, symprec=symprec).symbol)
atoms1: P 1
atoms2: P 4 m m
atoms3: P 1
atoms4: P 4 m m
このように FixSymmetry を適用した atoms2, atoms4 はP 4 m m 空間群を保っていますが、 atoms1, atoms3 は空間群が崩れ、一番対称性の低いP 1 になってしまっています。
ブラべー格子¶
空間群について説明を行ったので、関連する概念としてブラべー格子の説明をします。
空間群はatomsのセル及び原子配置双方に依存して決まる対称性ですが、ブラべー格子はセル(単位胞)のみから決まるものです。
ブラべー格子は以下の14種類のいずれかになることが知られています。 これら14種類は上記のwikipediaのリンクでも図示されているのでご確認ください。
[19]:
from ase.lattice import CUB, FCC, BCC, TET, BCT, HEX, RHL, ORC, ORCF, ORCI, ORCC, MCL, MCLC, TRI
print(" 1. CUB:", CUB.longname, ",", CUB.crystal_family)
print(" 2. FCC:", FCC.longname, ",", FCC.crystal_family)
print(" 3. BCC:", BCC.longname, ",", BCC.crystal_family)
print(" 4. TET:", TET.longname, ",", TET.crystal_family)
print(" 5. BCT:", BCT.longname, ",", BCT.crystal_family)
print(" 6. HEX:", HEX.longname, ",", HEX.crystal_family)
print(" 7. RHL:", RHL.longname, ",", RHL.crystal_family)
print(" 8. ORC:", ORC.longname, ",", ORC.crystal_family)
print(" 9. ORCF:", ORCF.longname, ",", ORCF.crystal_family)
print("10. ORCI:", ORCI.longname, ",", ORCI.crystal_family)
print("11. ORCC:", ORCC.longname, ",", ORCC.crystal_family)
print("12. MCL :", MCL.longname, ",", MCL.crystal_family)
print("13. MCLC:", MCLC.longname, ",", MCLC.crystal_family)
print("14. TRI :", TRI.longname, ",", TRI.crystal_family)
1. CUB: primitive cubic , cubic
2. FCC: face-centred cubic , cubic
3. BCC: body-centred cubic , cubic
4. TET: primitive tetragonal , tetragonal
5. BCT: body-centred tetragonal , tetragonal
6. HEX: primitive hexagonal , hexagonal
7. RHL: primitive rhombohedral , hexagonal
8. ORC: primitive orthorhombic , orthorhombic
9. ORCF: face-centred orthorhombic , orthorhombic
10. ORCI: body-centred orthorhombic , orthorhombic
11. ORCC: base-centred orthorhombic , orthorhombic
12. MCL : primitive monoclinic , monoclinic
13. MCLC: base-centred monoclinic , monoclinic
14. TRI : primitive triclinic , triclinic
ASEではget_bravais_lattice関数を用いてブラべー格子の判定を行うことができます。
[20]:
bto_tetra.cell.get_bravais_lattice()
[20]:
TET(a=4.0044570000000003773, c=4.2006360000000002586)
正方晶であるBaTiO3構造に対して、期待通りTETが得られました。
ここで注意すべき内容として、cellは単位胞 (primitive cell) を指定する必要があります。
以下Fe BCC構造を作成して、get_bravais_latticeを用いた際、単位胞を指定した場合は期待通りBCCが返って来ますが、 cubic=Trueとして立方体のユニットセルを作った構造に対してget_bravais_latticeを呼ぶとCUBが返ってきています。
[21]:
from ase.build import bulk
from pfcc_extras.visualize.ase import view_ase_atoms
fe_bcc = bulk("Fe")
view_ase_atoms(fe_bcc, figsize=(4, 4), title="Fe BCC atoms", scale=100, rotation="0x,0y,0z")
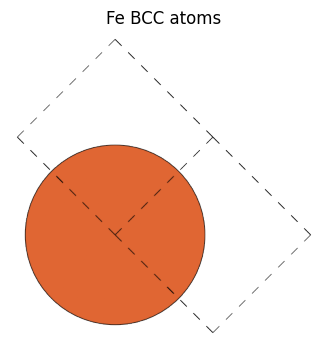
[22]:
# view_ngl(fe_bcc)
[23]:
print("fe_bcc Bravais lattice:", fe_bcc.cell.get_bravais_lattice())
print("fe_bcc cell :", fe_bcc.cell)
fe_bcc Bravais lattice: BCC(a=2.87)
fe_bcc cell : Cell([[-1.435, 1.435, 1.435], [1.435, -1.435, 1.435], [1.435, 1.435, -1.435]])
[24]:
fe_cubic = bulk("Fe", cubic=True)
view_ase_atoms(fe_cubic, figsize=(4, 4), title="Fe BCC cubic=True", scale=100, rotation="0x,0y,0z")
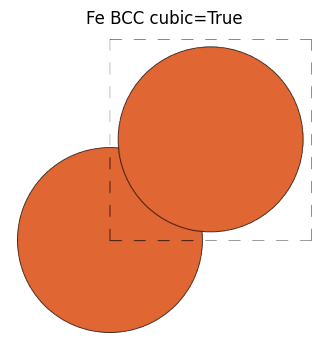
[25]:
# view_ngl(fe_cubic)
[26]:
print("fe_cubic Bravais lattice:", fe_cubic.cell.get_bravais_lattice())
print("fe_cubic cell :", fe_cubic.cell)
fe_cubic Bravais lattice: CUB(a=2.87)
fe_cubic cell : Cell([2.87, 2.87, 2.87])
参考文献¶
空間群について、より詳しく勉強したい方は以下が参考になるでしょう。
「物質の対称性と群論」 今野 豊彦