等圧等温(NPT)アンサンブル¶
TL;DR¶
NPT-MDシミュレーションでは圧力と温度が一定に制御される手法で、圧力制御(barostat)に関してASEではParrinello-Rahman法、Berendsen法の2種類の一般的な手法が存在。
用途としては固体や流体の熱膨張、相転移、加圧状態のシミュレーション等
Parrinello-Rahman法ではシミュレーションのセルの自由度が全て可変。pfactorを適切に設定する必要があり。
Berendsen barostatではBerendsen thermostatと同様、非常に効率的に収束性良く制御可能。Berendsen barostatはセルの角度は固定して各セル長を独立に可変、もしくは各セル長の比率を固定する2つのモードで計算可能。compressibilityを入力パラメーターとして適切に設定が必要。
本節では圧力と温度の両方が一定となるような平衡状態を作る計算手法について説明します。一般に圧力制御の仕組みはbarostatと呼ばれ、一般に6-2節で出てきた熱浴法(thermostat)と同時に用いることで等温等圧アンサンブル(isothermal-isobaric ensemble、またはNPT)と呼ばれる状態分布を生成することを目的としてます。NPT-MDシミュレーションで(原理的に)検討可能な現象には
固体の熱膨張率
融点の予測
固体の相転移
流体(ガス、液体)の密度予測
etc.
が考えられます。原理的にという枕詞がついている理由は、これらの現象の再現性は計算に用いる力場の精度に大きく依存するためで、特に小さなエネルギー差に依存する分子間力や流体の状態予測は非常に難しいことが知られているからです。本チュートリアルでは比較的精度が高いと考えられる固体の事例を通してNPT-MDについて学んでいきます。
まずは本チュートリアルで利用するASEに実装されているNPT-MDの手法について確認します。2022年6月現在、ASEで標準的に利用可能な実装は以下の3種類が存在します。
クラス名 |
ensemble |
パラメーター |
熱浴 |
圧力制御 |
コメント |
|---|---|---|---|---|---|
NPT |
NPT |
時定数(\(\tau_t\)),圧力因子(pfactor) |
Nosé–Hoover |
Parrinello-Rahman |
セルの全自由度が可変、制御可能 |
NPTBerendsen |
NPT |
\(\tau_t\),\(\tau_P\),\(\beta_T\) |
Berendsen |
Berendsen |
セル形状は維持し体積変化のみ |
InhomogeneousBerendsen |
NPT |
\(\tau_t\),\(\tau_P\),\(\beta_T\) |
Berendsen |
Berendsen |
セル角度は保持するが、圧力の異方性は考慮可能 |
表中の2番目と3番目の手法はBerendsen barostatで本質的に同じものです。(ちなみに3番目の手法であるInhomogeneousBerendsenはASEのマニュアルで記載はないのですが、NPTBerendsenとともにASEのなかでクラスが定義されています。)したがって、ASEのフレームワーク内で使える機能としてはParrinello-Rahman法とBerendsen法の2種類のみになります。熱浴自体は6-2節で解説した手法が用いられているので、これらの熱浴法の特徴をよく考慮する必要があります。
それではまず、系の自由度と汎用性が比較的高いParrinnello-Rahman法を見てみましょう。
Parrinello-Rahman法の運動方程式¶
Parrinello-Rahman法はいわゆる拡張系の計算手法で、Nosé–Hoover熱浴法の時のように、計算対象の系が仮想的に外部の一定温度、一定圧力の系と接続されていることを仮定します。この場合の運動方程式は下記のように記述されます。(導出の詳細については参考文献[1-3]をご確認ください。)
ここでNosé–Hoover熱浴以外の項に限定すると、圧力制御の時定数\(\tau_P\)、系の重心\(R_o\), 目標の外圧\(P_o\),シミュレーションセル体積\(V\)があります。\(\eta\)が圧力制御自由度を表す変数になっています。\(\mathbf{h} = (\mathbf{a}, \mathbf{b}, \mathbf{c})\)で\(\mathbf{a},\mathbf{b},\mathbf{c}\)はそれぞれシミュレーションセルの各辺を定義するセルベクトルです。
上記の方程式で温度\(T_o\)や圧力\(P_o\)以外にユーザーが設定しなければいけない値は\(\tau_T\)と\(\tau_P\)の2つがあります。それではまず、単純に\(\tau_T\)と\(\tau_P\)にを任意の値に設定した場合を以下に示します。ここで\(\tau_T\)を20 fsecとしています。\(\tau_P\)を直接指定しませんが、pfactorと呼ばれる値が\(\tau_P^2B\)となります。\(B\)はbulk modulusを指しており、この値をあらかじめ計算して指定する必要があります。しかし、\(\tau_P\)自体の正確な値が事前にわからないのでpfactorを特定する術がありません。また\(B\)の値も異方性を示す構造や異なるタイプの物質が混在する際は計算しようがありません。したがって、pfactorそのものの概ねの値を設定してbarostatの挙動を調べます。以下の例でも言及しますが、少なくとも金属の結晶系では約10\(^6\) GPa\(\cdot\)fs\(^2\) から10\(^7\) GPa\(\cdot\)fs\(^2\) のオーダーの値を用いると計算が安定して収束性も良いようです。それ以外の材料となる場合は、念のため事前検討として、pfactorの値を振ってみて体積変化の様子を確認しておくことをオススメします。
計算事例:熱膨張係数の計算¶
それではNPTアンサンブルの計算事例としてNosé–Hoover thermostatとParrinello-Rahman barostat(ASEのNPTクラス)を使って固体の熱膨張係数を計算してみます。温度を変化させながら熱平衡状態を作り出し、その時の格子定数の平均値から各温度における熱膨張係数を算出します。
今回は簡単のためfcc-Cuを用いて計算を行います。計算に用いられるスクリプトは以下のとおりです。温度は200 Kから1000 Kまで100 K刻み、外圧は1 barとします。対象の構造はfcc-Cuを3x3x3 unit cellsに拡張して108原子で計算を行います。以下では高速性のためASAP3-EMT力場を用いていますが、PFPで計算する場合も全く同様です。時間ステップは1 fsで20 psのシミュレーションで十分に平衡状態に達します。
[1]:
import ase
from ase.build import bulk
from ase.md.velocitydistribution import MaxwellBoltzmannDistribution,Stationary
from ase.md.npt import NPT
from ase.md import MDLogger
from ase import units
from time import perf_counter
calc_type = "EMT"
# calc_type = "PFP"
if calc_type == "EMT":
# ASAP3-EMT calculator
from asap3 import EMT
calculator = EMT()
elif calc_type == "PFP":
# PFP calculator
from pfp_api_client.pfp.estimator import Estimator, EstimatorCalcMode
from pfp_api_client.pfp.calculators.ase_calculator import ASECalculator
estimator = Estimator(calc_mode=EstimatorCalcMode.PBE, model_version="v8.0.0")
calculator = ASECalculator(estimator)
else:
raise ValueError(f"Wrong calc_type = {calc_type}!")
# Set up a crystal
atoms_in = bulk("Cu",cubic=True)
atoms_in *= 3
atoms_in.pbc = True
print("atoms_in = ",atoms_in)
# input parameters
time_step = 1.0 # fsec
#temperature = 300 # Kelvin
num_md_steps = 20000
num_interval = 10
sigma = 1.0 # External pressure in bar
ttime = 20.0 # Time constant in fs
pfactor = 2e6 # Barostat parameter in GPa
temperature_list = [200,300,400,500,600,700,800,900,1000]
# Print statements
def print_dyn():
imd = dyn.get_number_of_steps()
etot = atoms.get_total_energy()
temp_K = atoms.get_temperature()
stress = atoms.get_stress(include_ideal_gas=True)/units.GPa
stress_ave = (stress[0]+stress[1]+stress[2])/3.0
elapsed_time = perf_counter() - start_time
print(f" {imd: >3} {etot:.3f} {temp_K:.2f} {stress_ave:.2f} {stress[0]:.2f} {stress[1]:.2f} {stress[2]:.2f} {stress[3]:.2f} {stress[4]:.2f} {stress[5]:.2f} {elapsed_time:.3f}")
# run MD
for i,temperature in enumerate(temperature_list):
print("i,temperature = ",i,temperature)
print(f"sigma = {sigma:.1e} bar")
print(f"ttime = {ttime:.3f} fs")
print(f"pfactor = {pfactor:.3f} GPa*fs^2")
temperature_str = str(int(temperature)).zfill(4)
output_filename = f"./output/ch6/fcc-Cu_3x3x3_NPT_{calc_type}_{temperature_str}K"
log_filename = output_filename + ".log"
traj_filename = output_filename + ".traj"
print("log_filename = ",log_filename)
print("traj_filename = ",traj_filename)
atoms = atoms_in.copy()
atoms.calc = calculator
# Set the momenta corresponding to T=300K
MaxwellBoltzmannDistribution(atoms, temperature_K=temperature,force_temp=True)
Stationary(atoms)
dyn = NPT(atoms,
time_step*units.fs,
temperature_K = temperature,
externalstress = sigma*units.bar,
ttime = ttime*units.fs,
pfactor = pfactor*units.GPa*(units.fs**2),
logfile = log_filename,
trajectory = traj_filename,
loginterval=num_interval
)
print_interval = 1000 if calc_type == "EMT" else num_interval
dyn.attach(print_dyn, interval=print_interval)
dyn.attach(MDLogger(dyn, atoms, log_filename, header=True, stress=True, peratom=True, mode="a"), interval=num_interval)
# Now run the dynamics
start_time = perf_counter()
print(f" imd Etot(eV) T(K) stress(mean,xx,yy,zz,yz,xz,xy)(GPa) elapsed_time(sec)")
dyn.run(num_md_steps)
atoms_in = Atoms(symbols='Cu108', pbc=True, cell=[10.83, 10.83, 10.83])
i,temperature = 0 200
sigma = 1.0e+00 bar
ttime = 20.000 fs
pfactor = 2000000.000 GPa*fs^2
log_filename = ./output/ch6/fcc-Cu_3x3x3_NPT_EMT_0200K.log
traj_filename = ./output/ch6/fcc-Cu_3x3x3_NPT_EMT_0200K.traj
imd Etot(eV) T(K) stress(mean,xx,yy,zz,yz,xz,xy)(GPa) elapsed_time(sec)
0 2.727 200.00 1.64 1.62 1.66 1.63 -0.03 -0.00 0.04 0.004
1000 3.257 138.10 0.86 0.84 0.84 0.88 0.17 0.17 0.21 1.304
2000 4.444 192.41 0.77 0.61 0.92 0.79 0.29 0.27 -0.04 2.563
3000 4.381 187.60 0.93 1.03 0.94 0.84 0.12 0.08 0.30 3.808
4000 4.599 181.45 0.52 0.42 0.76 0.39 0.05 0.05 0.21 5.072
5000 5.692 202.32 -0.38 -0.38 -0.35 -0.41 -0.06 0.56 0.25 6.414
6000 6.109 220.68 -0.65 -0.74 -0.68 -0.52 -0.20 0.02 0.04 7.671
7000 5.639 219.03 -0.15 0.01 -0.36 -0.10 0.04 0.15 -0.01 8.902
8000 5.351 205.21 0.45 0.44 0.39 0.53 0.05 0.24 -0.04 10.165
9000 5.376 174.50 0.22 0.05 0.42 0.18 0.18 0.15 -0.17 11.484
10000 5.744 196.53 -0.33 -0.46 -0.25 -0.27 0.05 -0.02 0.09 12.785
11000 5.523 230.52 -0.30 -0.31 -0.43 -0.17 -0.00 0.05 0.15 14.047
12000 4.885 184.51 -0.11 -0.14 -0.08 -0.13 0.30 0.12 -0.05 15.302
13000 5.545 213.75 0.18 0.34 0.14 0.06 0.55 -0.12 0.03 16.610
14000 6.289 218.35 0.14 0.21 0.33 -0.12 0.33 0.25 0.12 17.857
15000 5.202 205.62 0.44 0.28 0.56 0.48 0.39 -0.08 -0.00 19.133
16000 5.704 211.51 -0.37 -0.55 -0.22 -0.34 0.05 -0.40 -0.18 20.411
17000 5.178 184.93 -0.52 -0.41 -0.71 -0.45 0.04 -0.17 -0.10 21.694
18000 5.410 192.98 -0.25 -0.03 -0.46 -0.27 0.08 -0.11 -0.26 22.949
19000 6.283 234.67 0.13 0.31 -0.06 0.15 -0.06 -0.20 -0.16 24.195
20000 5.147 180.81 0.62 0.69 0.56 0.60 -0.14 -0.20 -0.49 25.469
i,temperature = 1 300
sigma = 1.0e+00 bar
ttime = 20.000 fs
pfactor = 2000000.000 GPa*fs^2
log_filename = ./output/ch6/fcc-Cu_3x3x3_NPT_EMT_0300K.log
traj_filename = ./output/ch6/fcc-Cu_3x3x3_NPT_EMT_0300K.traj
imd Etot(eV) T(K) stress(mean,xx,yy,zz,yz,xz,xy)(GPa) elapsed_time(sec)
0 4.123 300.00 1.52 1.61 1.46 1.50 -0.01 -0.03 -0.01 0.002
1000 7.039 294.54 0.62 0.76 0.50 0.62 -0.02 -0.11 -0.11 1.289
2000 6.642 266.68 1.46 1.74 1.57 1.06 -0.25 0.02 0.05 2.559
3000 7.757 288.57 1.48 1.52 1.57 1.34 -0.15 -0.16 0.39 3.823
4000 8.489 291.95 0.31 0.34 -0.02 0.61 0.08 -0.08 0.58 5.096
5000 8.163 265.87 -0.89 -1.07 -1.04 -0.57 0.11 0.19 0.65 6.381
6000 8.944 336.60 -1.32 -1.24 -1.20 -1.53 0.20 0.60 0.37 7.666
7000 7.524 257.73 -0.28 -0.18 -0.06 -0.62 -0.13 0.11 0.52 8.908
8000 8.845 311.11 0.50 0.57 0.61 0.32 0.21 0.36 0.73 10.169
9000 8.675 306.12 1.05 1.08 0.82 1.24 0.52 0.10 0.73 11.489
10000 8.658 313.89 0.58 0.47 0.39 0.87 0.74 0.14 0.74 12.752
11000 9.631 395.51 -0.49 -0.43 -0.62 -0.41 0.52 0.40 0.70 13.999
12000 8.691 286.93 -1.19 -0.96 -1.09 -1.52 0.28 0.22 0.49 15.278
13000 7.403 260.96 -0.60 -0.56 -0.29 -0.95 0.51 -0.03 0.44 16.553
14000 9.016 325.97 -0.14 -0.04 -0.17 -0.21 0.54 -0.07 0.80 17.834
15000 9.425 316.12 0.55 0.62 0.28 0.76 0.44 0.02 0.89 19.086
16000 8.362 287.70 0.83 0.60 0.85 1.05 0.38 0.08 0.89 20.360
17000 8.799 292.57 -0.21 -0.49 0.24 -0.37 -0.02 -0.38 0.91 21.664
18000 8.024 293.51 -0.65 -0.50 -0.71 -0.73 -0.23 0.08 1.02 22.930
19000 8.160 303.79 -0.84 -0.47 -1.30 -0.73 -0.11 -0.19 1.18 24.190
20000 9.328 351.21 -0.45 -0.40 -0.89 -0.06 -0.17 -0.22 1.09 25.461
i,temperature = 2 400
sigma = 1.0e+00 bar
ttime = 20.000 fs
pfactor = 2000000.000 GPa*fs^2
log_filename = ./output/ch6/fcc-Cu_3x3x3_NPT_EMT_0400K.log
traj_filename = ./output/ch6/fcc-Cu_3x3x3_NPT_EMT_0400K.traj
imd Etot(eV) T(K) stress(mean,xx,yy,zz,yz,xz,xy)(GPa) elapsed_time(sec)
0 5.519 400.00 1.40 1.47 1.33 1.41 -0.07 0.04 -0.06 0.003
1000 11.615 433.05 -1.87 -1.41 -2.02 -2.19 -0.34 -0.03 -0.12 1.265
2000 12.383 419.09 -0.11 0.46 0.03 -0.82 -0.31 -0.01 0.22 2.529
3000 11.877 413.81 2.05 2.38 2.37 1.39 -0.11 0.04 -0.28 3.805
4000 11.944 409.88 2.15 1.89 2.46 2.11 0.18 -0.01 -0.21 5.076
5000 11.040 381.69 0.96 0.81 0.82 1.26 0.10 -0.00 0.60 6.369
6000 10.106 394.10 -0.40 -0.22 -1.01 0.04 -0.02 -0.30 0.23 7.647
7000 10.675 424.80 -1.73 -1.60 -1.97 -1.60 -0.13 -0.82 0.54 8.945
8000 11.052 382.51 -1.81 -1.64 -1.59 -2.21 -0.24 -0.54 -0.04 10.224
9000 11.590 414.92 -0.36 -0.14 -0.16 -0.79 -0.56 -0.64 0.28 11.498
10000 10.523 341.87 1.38 1.67 1.18 1.27 -0.14 -0.24 0.33 12.762
11000 10.769 359.31 1.98 2.01 1.77 2.15 0.27 -0.08 0.19 14.014
12000 11.827 390.91 0.78 0.84 0.67 0.81 0.17 -0.72 0.01 15.283
13000 11.848 448.43 -0.54 -0.82 -0.11 -0.68 0.49 -0.85 0.76 16.570
14000 10.131 371.62 -1.29 -1.31 -0.92 -1.64 -0.22 -0.86 0.65 17.851
15000 10.884 413.01 -1.32 -1.05 -1.42 -1.49 0.33 -0.59 0.60 19.117
16000 10.524 347.84 -0.50 -0.26 -1.03 -0.22 0.27 -1.27 0.16 20.391
17000 12.336 410.07 0.30 0.30 0.49 0.11 0.38 -0.29 0.34 21.652
18000 11.884 372.32 1.41 0.92 2.28 1.03 0.50 -0.44 0.32 22.936
19000 11.505 398.81 1.77 1.47 2.62 1.22 -0.01 -0.95 0.20 24.188
20000 11.140 403.94 0.67 0.88 0.21 0.92 -0.05 -0.59 -0.48 25.481
i,temperature = 3 500
sigma = 1.0e+00 bar
ttime = 20.000 fs
pfactor = 2000000.000 GPa*fs^2
log_filename = ./output/ch6/fcc-Cu_3x3x3_NPT_EMT_0500K.log
traj_filename = ./output/ch6/fcc-Cu_3x3x3_NPT_EMT_0500K.traj
imd Etot(eV) T(K) stress(mean,xx,yy,zz,yz,xz,xy)(GPa) elapsed_time(sec)
0 6.915 500.00 1.29 1.31 1.29 1.27 0.05 -0.06 -0.06 0.003
1000 12.058 479.42 -1.63 -1.76 -1.58 -1.57 -0.08 0.32 0.65 1.308
2000 12.707 510.71 0.12 -0.36 0.33 0.38 -0.04 0.75 -0.04 2.558
3000 15.222 539.00 1.53 1.90 1.36 1.32 -0.24 0.64 0.21 3.825
4000 14.956 487.91 3.19 3.80 2.80 2.96 -0.11 0.89 0.05 5.093
5000 16.151 489.16 3.07 2.97 3.59 2.64 -0.13 0.75 0.43 6.351
6000 15.795 561.85 2.81 2.43 3.07 2.93 -0.09 0.32 0.57 7.608
7000 13.226 489.39 1.42 1.18 1.52 1.56 0.09 0.27 -0.35 8.856
8000 13.933 547.11 -1.62 -1.45 -1.61 -1.79 0.01 0.47 -0.56 10.128
9000 14.159 497.65 -3.89 -3.67 -3.95 -4.06 0.13 0.59 -0.26 11.450
10000 13.296 480.78 -3.69 -3.94 -4.40 -2.74 0.40 0.33 -0.59 12.716
11000 13.504 483.52 -1.88 -2.03 -1.77 -1.84 0.84 0.56 -0.95 13.992
12000 13.670 457.77 0.13 0.35 0.23 -0.19 0.59 0.35 -0.08 15.287
13000 15.112 553.76 1.80 2.25 2.06 1.09 -0.05 0.72 -0.22 16.557
14000 16.743 627.12 2.40 2.63 2.49 2.08 -0.45 0.90 -0.51 17.804
15000 15.498 497.26 1.54 1.58 0.95 2.11 -0.65 0.32 -0.69 19.082
16000 15.301 539.67 0.45 0.58 0.41 0.37 -0.98 0.72 -0.48 20.359
17000 13.511 481.97 -0.65 -0.70 -0.12 -1.12 -1.35 1.57 0.06 21.635
18000 13.369 510.93 -1.23 -1.77 -1.05 -0.89 -1.19 0.50 -0.89 22.896
19000 14.594 496.53 -1.81 -2.12 -1.74 -1.58 -0.90 0.74 -1.54 24.173
20000 15.085 526.83 -0.78 -0.43 -1.62 -0.30 -0.67 0.92 -1.49 25.436
i,temperature = 4 600
sigma = 1.0e+00 bar
ttime = 20.000 fs
pfactor = 2000000.000 GPa*fs^2
log_filename = ./output/ch6/fcc-Cu_3x3x3_NPT_EMT_0600K.log
traj_filename = ./output/ch6/fcc-Cu_3x3x3_NPT_EMT_0600K.traj
imd Etot(eV) T(K) stress(mean,xx,yy,zz,yz,xz,xy)(GPa) elapsed_time(sec)
0 8.311 600.00 1.17 1.19 1.10 1.22 0.08 0.09 -0.13 0.002
1000 16.715 639.49 -5.01 -5.06 -5.46 -4.52 -0.26 -0.47 0.74 1.303
2000 15.139 488.07 -3.46 -3.57 -2.82 -3.99 0.14 -0.38 0.28 2.560
3000 15.724 510.99 -1.76 -1.63 -1.54 -2.11 0.32 0.23 0.14 3.810
4000 16.667 522.17 0.37 0.60 -0.06 0.57 -0.36 -0.75 1.05 5.093
5000 18.164 650.39 2.68 2.97 2.22 2.85 -0.26 -0.78 0.92 6.374
6000 18.164 554.33 3.50 3.53 2.99 3.97 -0.77 -0.83 0.67 7.659
7000 19.922 612.39 3.45 2.91 3.91 3.53 -0.73 -0.73 0.64 8.943
8000 19.457 526.47 2.56 2.06 3.09 2.53 -0.23 -0.41 -0.55 10.209
9000 18.140 513.53 1.80 1.78 1.80 1.83 -1.00 -0.53 0.31 11.515
10000 17.600 607.37 0.94 1.48 0.55 0.80 -1.20 -1.21 0.11 12.790
11000 16.172 524.88 -0.22 0.67 -0.72 -0.61 -0.27 -1.12 0.01 14.088
12000 18.702 704.78 -2.61 -3.05 -2.36 -2.43 0.12 -1.60 -0.33 15.368
13000 15.189 575.25 -2.38 -3.59 -1.61 -1.94 -0.24 -1.21 0.17 16.688
14000 16.155 612.83 -3.26 -3.77 -2.91 -3.10 -0.55 -0.88 -0.32 18.012
15000 16.451 596.63 -3.31 -2.66 -3.83 -3.43 0.09 -1.52 -0.10 19.394
16000 17.787 637.60 -2.79 -1.81 -3.53 -3.04 -0.18 -1.36 0.63 20.652
17000 17.834 671.97 -1.26 -1.60 -1.14 -1.05 -0.11 -1.15 0.35 21.921
18000 16.050 601.58 1.16 0.87 1.07 1.55 -0.44 -0.31 -0.03 23.190
19000 17.458 565.19 2.00 1.70 2.47 1.83 -0.77 -0.42 -0.06 24.472
20000 19.233 635.18 2.36 2.81 2.15 2.12 -0.59 -1.00 0.24 25.751
i,temperature = 5 700
sigma = 1.0e+00 bar
ttime = 20.000 fs
pfactor = 2000000.000 GPa*fs^2
log_filename = ./output/ch6/fcc-Cu_3x3x3_NPT_EMT_0700K.log
traj_filename = ./output/ch6/fcc-Cu_3x3x3_NPT_EMT_0700K.traj
imd Etot(eV) T(K) stress(mean,xx,yy,zz,yz,xz,xy)(GPa) elapsed_time(sec)
0 9.707 700.00 1.05 1.03 1.06 1.07 -0.08 -0.00 0.03 0.003
1000 20.383 739.14 -6.27 -5.74 -6.45 -6.63 0.11 0.36 -0.11 1.265
2000 19.614 696.89 -6.22 -5.47 -5.62 -7.56 0.29 0.43 -1.10 2.558
3000 17.879 652.89 -5.55 -5.02 -6.08 -5.54 0.78 0.43 -0.62 3.849
4000 19.976 694.34 -5.85 -6.30 -5.76 -5.50 1.30 0.36 -1.03 5.157
5000 20.035 673.12 -4.74 -5.06 -4.43 -4.75 1.29 0.12 -1.36 6.480
6000 20.622 645.33 -4.34 -4.75 -4.44 -3.84 0.60 0.24 -1.02 7.770
7000 19.666 627.41 -2.91 -2.72 -2.87 -3.16 0.41 -0.44 -1.34 9.066
8000 20.864 688.49 -2.25 -2.65 -1.63 -2.47 -0.17 -0.95 -1.13 10.364
9000 19.112 668.93 -0.62 -1.02 -0.78 -0.06 0.72 -0.62 -0.18 11.647
10000 20.284 699.50 -0.60 -1.47 -0.61 0.27 0.34 -0.59 -1.20 12.932
11000 19.498 697.73 0.77 1.59 0.63 0.10 1.27 0.18 0.07 14.195
12000 21.804 792.85 0.47 0.80 0.65 -0.04 -0.10 -0.18 0.28 15.469
13000 20.735 697.89 1.26 0.53 1.39 1.87 -0.02 1.01 0.63 16.741
14000 21.382 740.21 1.76 0.94 2.24 2.11 -0.77 0.17 0.04 18.031
15000 21.828 746.62 1.74 2.42 2.27 0.53 -0.53 -0.43 0.27 19.315
16000 22.004 746.30 1.52 1.97 1.16 1.41 -0.27 0.18 -0.14 20.603
17000 21.624 707.25 2.07 1.80 2.24 2.17 -0.22 -0.50 0.33 21.897
18000 21.128 685.74 2.77 2.07 2.31 3.92 -1.22 -1.43 0.32 23.188
19000 22.819 730.49 2.48 2.62 2.59 2.22 0.09 -1.54 0.20 24.495
20000 23.259 716.84 1.97 2.45 2.53 0.91 -1.07 -1.18 1.08 25.810
i,temperature = 6 800
sigma = 1.0e+00 bar
ttime = 20.000 fs
pfactor = 2000000.000 GPa*fs^2
log_filename = ./output/ch6/fcc-Cu_3x3x3_NPT_EMT_0800K.log
traj_filename = ./output/ch6/fcc-Cu_3x3x3_NPT_EMT_0800K.traj
imd Etot(eV) T(K) stress(mean,xx,yy,zz,yz,xz,xy)(GPa) elapsed_time(sec)
0 11.103 800.00 0.94 0.98 0.71 1.12 0.07 -0.06 0.09 0.003
1000 21.812 762.85 -6.73 -7.25 -6.65 -6.28 -1.23 -0.22 1.20 1.330
2000 23.271 804.18 -5.51 -6.51 -5.45 -4.57 -0.74 -2.03 2.05 2.610
3000 22.495 854.60 -4.24 -4.14 -4.29 -4.28 -0.35 -1.89 2.23 3.875
4000 22.232 796.81 -4.12 -3.80 -4.61 -3.94 0.86 -1.16 1.89 5.140
5000 19.335 764.45 -3.01 -3.04 -3.62 -2.37 1.60 -1.86 1.44 6.398
6000 21.821 797.04 -3.90 -4.50 -4.51 -2.71 1.97 -1.15 0.52 7.658
7000 21.947 772.94 -3.83 -3.48 -3.17 -4.83 1.76 0.10 -0.18 8.944
8000 21.421 765.09 -1.84 -0.79 -2.21 -2.52 0.80 0.48 -0.44 10.271
9000 22.487 823.21 -2.53 -1.80 -3.36 -2.43 0.48 0.16 0.25 11.551
10000 21.713 739.08 -1.72 -2.04 -1.70 -1.42 0.53 -0.28 0.16 12.830
11000 21.970 780.25 -0.64 -1.54 0.07 -0.45 -0.15 0.18 0.79 14.114
12000 21.425 665.58 -0.96 -1.23 -1.28 -0.35 0.06 0.38 -0.38 15.384
13000 20.883 650.72 0.13 0.77 -0.66 0.26 0.05 -0.42 0.02 16.655
14000 23.596 730.13 -0.27 -0.44 -0.71 0.35 -0.21 0.58 -1.00 17.939
15000 24.202 919.02 0.67 -0.22 0.52 1.70 0.82 0.45 -0.51 19.193
16000 24.128 778.05 0.16 -0.05 0.31 0.23 0.61 0.11 -0.13 20.468
17000 23.397 772.12 0.71 0.22 0.61 1.30 -0.09 0.09 0.26 21.757
18000 22.849 721.08 1.34 1.05 1.44 1.54 -0.17 0.64 1.09 23.043
19000 22.964 790.61 2.41 2.39 2.93 1.90 0.35 -0.16 -0.35 24.327
20000 24.617 749.05 1.23 1.33 1.37 1.00 0.72 0.06 0.23 25.591
i,temperature = 7 900
sigma = 1.0e+00 bar
ttime = 20.000 fs
pfactor = 2000000.000 GPa*fs^2
log_filename = ./output/ch6/fcc-Cu_3x3x3_NPT_EMT_0900K.log
traj_filename = ./output/ch6/fcc-Cu_3x3x3_NPT_EMT_0900K.traj
imd Etot(eV) T(K) stress(mean,xx,yy,zz,yz,xz,xy)(GPa) elapsed_time(sec)
0 12.499 900.00 0.82 0.81 0.90 0.75 0.10 -0.12 0.16 0.002
1000 23.423 834.16 -5.48 -6.79 -4.12 -5.52 -1.85 -0.69 1.58 1.337
2000 23.551 702.51 -2.86 -1.33 -3.18 -4.07 -1.04 -1.06 0.65 2.623
3000 27.744 907.63 0.38 0.00 -0.17 1.30 -0.08 -0.11 -0.75 3.884
4000 30.761 1002.33 3.16 2.31 3.78 3.40 -0.91 -0.75 -0.76 5.148
5000 33.001 998.32 2.50 2.02 3.62 1.87 0.09 -0.09 -0.45 6.405
6000 26.167 889.54 5.11 5.60 4.35 5.40 0.57 0.13 -0.48 7.676
7000 27.386 819.39 1.05 0.35 1.40 1.41 -0.35 -1.14 -0.54 8.949
8000 28.113 939.13 -0.24 -0.23 0.26 -0.75 -0.45 -0.45 0.91 10.217
9000 26.405 857.33 -0.70 0.41 -1.43 -1.08 -0.39 -0.53 0.79 11.499
10000 26.892 942.46 -1.89 -2.63 -2.42 -0.61 -0.14 -1.94 0.37 12.838
11000 28.269 995.74 -2.46 -3.68 -1.60 -2.09 -0.38 -1.49 0.73 14.126
12000 25.656 911.10 -1.00 -0.80 -0.72 -1.48 -0.10 -0.47 -0.16 15.392
13000 23.297 829.65 -0.23 0.43 -1.10 -0.02 -0.47 -0.32 -1.17 16.689
14000 25.628 898.60 0.28 0.51 0.28 0.03 -1.44 0.16 -1.20 17.956
15000 29.209 954.23 0.30 0.99 -0.21 0.13 -0.66 1.20 -1.12 19.225
16000 28.266 871.95 1.20 0.24 0.94 2.42 -0.44 0.29 -0.51 20.499
17000 28.500 866.69 1.15 0.89 1.41 1.17 -1.73 1.10 0.47 21.782
18000 27.243 832.05 -0.32 -0.36 -0.53 -0.06 -0.24 -0.07 0.67 23.041
19000 25.141 827.97 0.34 -0.02 -0.02 1.07 0.53 -0.12 0.41 24.301
20000 24.780 876.77 0.83 0.75 1.41 0.31 0.58 -0.45 -0.21 25.591
i,temperature = 8 1000
sigma = 1.0e+00 bar
ttime = 20.000 fs
pfactor = 2000000.000 GPa*fs^2
log_filename = ./output/ch6/fcc-Cu_3x3x3_NPT_EMT_1000K.log
traj_filename = ./output/ch6/fcc-Cu_3x3x3_NPT_EMT_1000K.traj
imd Etot(eV) T(K) stress(mean,xx,yy,zz,yz,xz,xy)(GPa) elapsed_time(sec)
0 13.895 1000.00 0.70 0.68 0.51 0.92 0.04 0.23 0.05 0.003
1000 29.676 928.19 -1.05 -1.83 0.19 -1.51 -1.12 0.72 -0.98 1.272
2000 33.128 1019.15 3.40 2.67 3.02 4.50 -0.63 1.02 -0.71 2.573
3000 35.329 1095.80 2.48 2.75 2.07 2.64 -1.08 1.38 -0.90 3.839
4000 31.810 1123.02 2.62 3.24 2.82 1.79 1.44 -0.16 -0.51 5.101
5000 32.830 1021.26 -2.58 -3.34 -2.37 -2.03 0.63 -0.60 3.17 6.380
6000 30.141 1113.73 -2.32 -2.18 -0.73 -4.04 -1.26 -1.62 1.31 7.648
7000 27.907 1047.10 -1.15 -0.14 -1.61 -1.71 -3.16 -1.67 1.65 8.931
8000 29.092 927.81 0.49 -0.38 -0.45 2.30 -1.93 -1.12 -0.04 10.200
9000 31.791 1071.16 0.44 0.48 0.67 0.18 -1.39 -0.41 -1.43 11.485
10000 30.929 1097.08 0.94 1.53 0.96 0.31 0.74 0.44 -0.87 12.740
11000 29.986 970.88 -0.02 -0.91 0.39 0.48 0.31 0.12 -0.64 14.001
12000 30.553 1083.88 -0.05 -0.12 0.48 -0.49 0.31 -0.27 -0.03 15.300
13000 30.370 994.91 -1.09 0.94 -2.24 -1.97 0.71 1.20 -0.35 16.600
14000 29.714 965.39 -0.41 -0.16 -0.50 -0.57 1.37 0.34 -0.07 17.892
15000 30.014 1041.61 0.15 0.29 -0.25 0.43 0.72 0.66 0.54 19.186
16000 30.035 1015.43 0.03 -0.76 0.76 0.07 0.17 0.29 -0.32 20.476
17000 29.797 963.30 0.34 0.45 -0.21 0.78 -1.20 -0.02 0.43 21.755
18000 30.446 962.12 0.94 1.05 0.33 1.44 -0.63 -0.22 1.30 23.051
19000 30.178 1023.73 0.53 0.16 0.66 0.77 0.18 -1.06 0.20 24.336
20000 29.661 950.11 -0.71 -1.22 -0.59 -0.33 -0.73 -2.03 0.06 25.601
結果を可視化してみると以下のようになります。
ここではread関数に index="::100" を指定することでTrajectoryファイルから間隔を間引いた結果に対して可視化しています。 Cuは固体の構造を保っており、大きく動いているわけではありませんが、振動の動きによりセルサイズに変化があることがわかります。
[2]:
from ase.io import Trajectory, read
from pfcc_extras.visualize.povray import traj_to_apng
from IPython.display import Image
traj = read("./output/ch6/fcc-Cu_3x3x3_NPT_EMT_0900K.traj", index="::100")
traj_to_apng(traj, f"output/ch6/Fig6-3_fcc-Cu_3x3x3_NPT_EMT_0900K.png", rotation="10x,-10y,0z", clean=True, n_jobs=16)
Image(url="output/ch6/Fig6-3_fcc-Cu_3x3x3_NPT_EMT_0900K.png")
[Parallel(n_jobs=16)]: Using backend ThreadingBackend with 16 concurrent workers.
[Parallel(n_jobs=16)]: Done 12 out of 21 | elapsed: 5.8s remaining: 4.4s
[Parallel(n_jobs=16)]: Done 21 out of 21 | elapsed: 7.2s finished
[2]:
[3]:
from ase.io import Trajectory, read
from pfcc_extras.visualize.view import view_ngl
traj = read("./output/ch6/fcc-Cu_3x3x3_NPT_EMT_0900K.traj", index="::100")
view_ngl(traj, replace_structure=True)
[3]:
熱浴の時定数\(\tau_t\)は20 fs、圧力制御パラメーターであるpfactorは2e6 GPa\(\cdot\)fs\(^2\)としています。上記の計算条件で熱平衡状態にするため300 Kで20 psのNPT-MDシミュレーションを行った際のセル体積の時間変化の様子を確認してみましょう。以下のようなコードで特定温度におけるMDシミュレーションの結果であるtrajファイルを解析出来ます。
[4]:
import matplotlib.pyplot as plt
from pathlib import Path
from ase.io import read,Trajectory
time_step = 0.01 # Time step size in ps between each snapshots recorded in traj
traj = Trajectory("./output/ch6/fcc-Cu_3x3x3_NPT_EMT_0300K.traj")
time = [ i*time_step for i in range(len(traj)) ]
volume = [ atoms.get_volume() for atoms in traj ]
# Create graph
fig = plt.figure(figsize=(8,3))
ax = fig.add_subplot(1, 1, 1)
ax.set_xlabel('time (ps)') # x axis label
ax.set_ylabel('Cell volume (Å^3)') # y axis label
ax.plot(time,volume, alpha=0.5)
ax.set_ylim([1100,1400])
#plt.savefig("filename.png") # Set filename to be saved
plt.show()
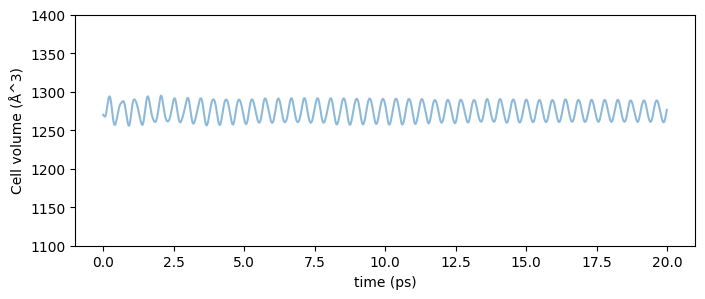
上記コードを実行すると、以下のような解析結果が得られます。
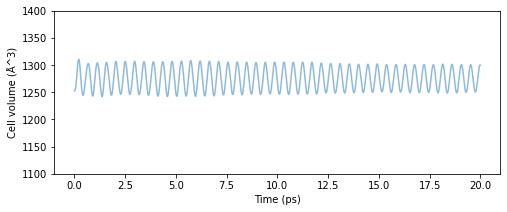
Fig.6-3a. Time evolution of cell volume. (fcc-Cu_3x3x3, @300 K and 1 bar)
NPTアンサンブルで計算することでセル体積が約4%程の範囲で振動することが見て取れます。今回の計算対象は立方晶であるため、この体積の幾何平均から結晶の格子定数を計算出来ます。200 Kから1000 Kまで実行し、その各温度での規格化した格子定数の平均値をプロットすると以下の結果が得られます。(平衡状態に達したあとの格子定数を計算したいため、np.mean(vol[int(len(vol)/2):])**(1/3) の部分では、Trajectoryの後半半分のみを使用して、体積から格子定数を計算しています。)
[5]:
import matplotlib.pyplot as plt
import numpy as np
from pathlib import Path
from ase.io import read,Trajectory
time_step = 10.0 # Time step size between each snapshots recorded in traj
paths = Path("./output/ch6/").glob(f"**/fcc-Cu_3x3x3_NPT_{calc_type}_*K.traj")
path_list = sorted([ p for p in paths ])
# Temperature list extracted from the filename
temperature = [ float(p.stem.split("_")[-1].replace("K","")) for p in path_list ]
print("temperature = ",temperature)
# Compute lattice parameter
lat_a = []
for path in path_list:
print(f"path = {path}")
traj = Trajectory(path)
vol = [ atoms.get_volume() for atoms in traj ]
lat_a.append(np.mean(vol[int(len(vol)/2):])**(1/3))
print("lat_a = ",lat_a)
# Normalize relative to the value at 300 K
norm_lat_a = lat_a/lat_a[1]
print("norm_lat_a = ",norm_lat_a)
# Plot
fig = plt.figure(figsize=(4,4))
ax = fig.add_subplot(1, 1, 1)
ax.set_xlabel('Temperature (K)') # x axis label
ax.set_ylabel('Normalized lattice parameter') # y axis label
ax.scatter(temperature[:len(norm_lat_a)],norm_lat_a, alpha=0.5,label=calc_type.lower())
ax.legend(loc="upper left")
temperature = [200.0, 300.0, 400.0, 500.0, 600.0, 700.0, 800.0, 900.0, 1000.0]
path = output/ch6/fcc-Cu_3x3x3_NPT_EMT_0200K.traj
path = output/ch6/fcc-Cu_3x3x3_NPT_EMT_0300K.traj
path = output/ch6/fcc-Cu_3x3x3_NPT_EMT_0400K.traj
path = output/ch6/fcc-Cu_3x3x3_NPT_EMT_0500K.traj
path = output/ch6/fcc-Cu_3x3x3_NPT_EMT_0600K.traj
path = output/ch6/fcc-Cu_3x3x3_NPT_EMT_0700K.traj
path = output/ch6/fcc-Cu_3x3x3_NPT_EMT_0800K.traj
path = output/ch6/fcc-Cu_3x3x3_NPT_EMT_0900K.traj
path = output/ch6/fcc-Cu_3x3x3_NPT_EMT_1000K.traj
lat_a = [10.821187657763522, 10.84284171781325, 10.866195382765163, 10.88834101681545, 10.91184951417741, 10.937661285868403, 10.958914931081702, 10.988423059467703, 11.016341565694251]
norm_lat_a = [0.99800292 1. 1.00215383 1.00419625 1.00636436 1.0087449
1.01070505 1.01342649 1.01600133]
[5]:
<matplotlib.legend.Legend at 0x7f2643b7a210>
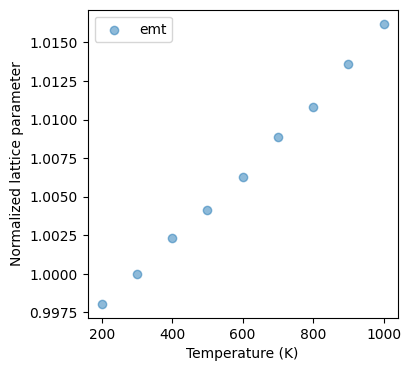
上記のコードを実行すると以下のようなプロットが得られます。
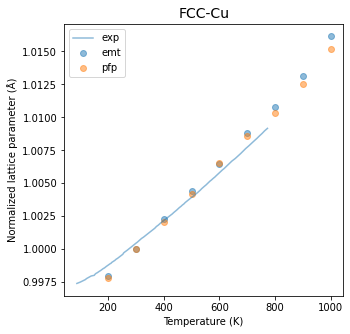
Fig.6-3b. Normalized lattice parameter as a function of temperature.
Experimental data is taken from Reference [4].
この結果にはさらにPFPを用いた計算結果、および参考までに実験値を比較対象としています。EMTおよびPFPのデータ共に非常に良い一致を示しており、小さな差ではありますがPFPはより実験値に近い傾向を示しています。
この規格化した格子定数の温度依存性から線熱膨張係数(CTE、\(\alpha\))を以下の関係式をもちいて算出します。
ここで\(\alpha\)が線熱膨張係数で、\(a(T)\)と\(a_{RT}\)は温度\(T\)と室温における格子定数です。以下がASAP3-EMT、PFP、実験値[4]のサマリーです。
\(\alpha\) ( \(10^{-5}\) /K) |
|
|---|---|
emt |
2.23 |
pfp |
2.13 |
exp |
1.74 |
計算誤差を考えると、いずれの計算結果も実験値とリーズナブルな範囲で一致していると考えてよいと思います。
このような手法でNPTアンサンブルのMDシミュレーションを用いることによって熱膨張係数を算出することが可能です。
最後に補足として言及しますと、「液体や気体の熱膨張も同様の手法で再現できるのでは?」と考えるかと思います。原理的には確かにその通りなのですが、現時点では再現性の良いモデルというのは限定的と思われます。古典力場で特定の液体や気体のみに特化したモデルは存在するのかもしれませんが、第一原理計算を用いた場合、液体や気体では固体に比べて非常に小さい分子間相互作用の精度が重要になり、現在ではそのような精度の量子化学計算自体が非常に困難です。特にNNPを作成する際には膨大な計算データが必要になり、高精度な量子化学計算を多量に行うのは現時点であまり現実的ではありません。従って今後この領域での精度が高いモデルの開発が期待されるところです。
[Advanced] Parrinello-Rahman barostatのパラメーター依存性¶
NPTアンサンブルでのMDシミュレーションを行う際にpfactorというパラメーターを設定する必要があり、適切な値の範囲が 10\(^6\) GPa\(\cdot\)fs\(^2\)から10\(^7\) GPa\(\cdot\)fs\(^2\)付近という説明がありました。ご参考までにpfactorの値を変化し際の結果を以下に示します。計算対象は上記と同じfcc-Cuの3x3x3 unit cellsで、温度は300 Kです。
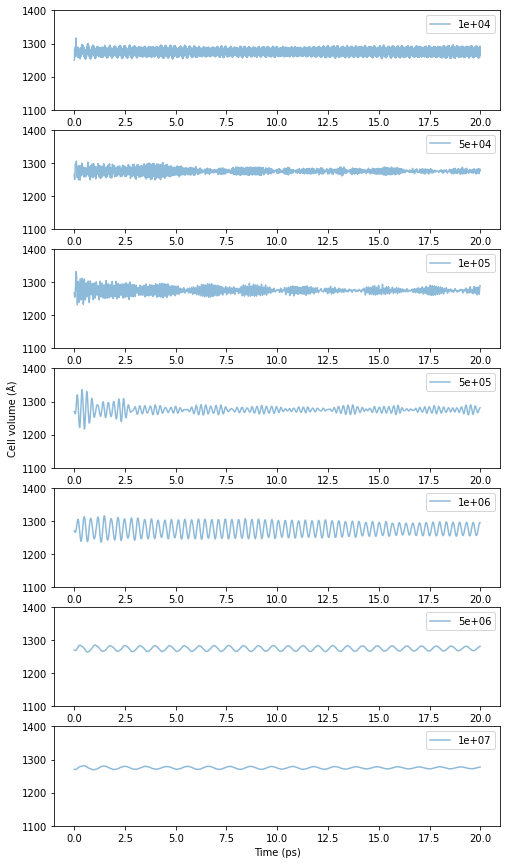
Fig.6-3c. Time evolution of cell volume as a function of pfactor.
pfactorが小さい領域では高速でセル体積が振動しており、高周波と低周波の振動が混在していて挙動が不安定な領域もあるのであまり好ましくありません。pfactorが大きくなるにつれて振動の周期が徐々に長くなり、小さなpfactorの計算初期で起きるの大きなセル体積の変化も殆ど見られません。明確にpfactorのどの値から使うと良いという指標があるわけではないですが、10\(^6\) Ga\(\cdot\)fsec\(^2\)以上であれば小さな振動は確認できるものの中央値は相変わらず安定しているようです。上限についても同様で明確な基準はなく、pfactorが大きいと振動周期が長くなり扱いづらいので、上記の例に関していえば10\(^6\)から10\(^7\)ぐらいが妥当な領域かと考えます。
[Advanced] Berendsen barostatのパラメーター依存性¶
Berendsen barostatを用いた計算方法について説明します。Berendsen barostatは以下の方程式に従って圧力の時間発展が計算されます。(導出の詳細は参考文献[5]をご覧ください。)
上式から明らかなように、Berendsen圧力制御法では指数関数的に系の各瞬間における圧力を外圧\(\mathbf{P}_o\)に近づけていきます。その速度は時定数\(\tau_P\)により制御されます。
各MDステップ毎に、各原子の座標とセルベクトルは以下の式で表される係数でスケーリングされます。
熱浴のコントロールの際に\(\tau_T\)が時定数だったように、圧力制御法でも適切な時定数\({\tau_P}\)を設定してやる必要があります。それでは実際の計算事例を見てみましょう。
ASEの機能であるNPTBerendsenクラスを用いるとdynamicsを定義するオブジェクトは以下の形で記述されます。
[6]:
from ase.md.nptberendsen import NPTBerendsen
dyn = NPTBerendsen(
atoms,
time_step*units.fs,
temperature_K = temperature,
pressure_au = 1.0 * units.bar,
taut = 5.0 * units.fs,
taup = 500.0 * units.fs,
compressibility_au = 5e-7 / units.bar,
logfile = log_filename,
trajectory = traj_filename,
loginterval=num_interval
)
圧力の異方性を考慮できるInhomogeneous_NPTBerendsenもほぼ同様の設定です。(クラス名をNPTBerendsenからInhomogeneous_NPTBerendsenとすることで利用可能です。)1点異なるのはmaskが設定でき、mask=(1, 1, 1)とするとa,b,c方向全て独立して変化可能です。このtupleの要素を0と設定することでその方向でcellが固定されます。
いずれのBerendsen barostatでも注意が必要なのは温度、圧力のような計算条件以外に、圧力制御時定数(taup、\(\tau_P\))や圧縮率(compressibility、\(\beta_T\))と呼ばれるパラメーターを設定する必要があることです。それぞれの値に対するセル体積の時間変化の依存性を300 Kにおけるfcc-Cuの例を用いて確認します。まずは\(\tau_P\)の方からみてみます。
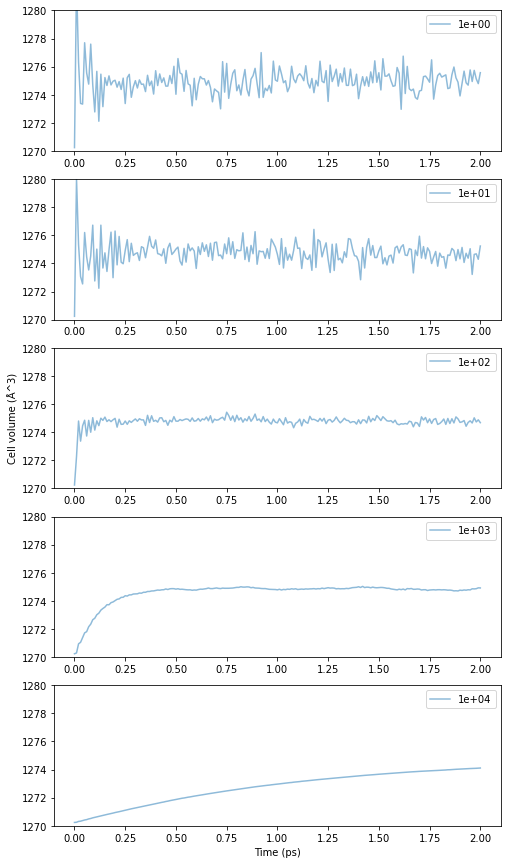
Fig.6-3d. Time evolution of cell volume as a function of \(\tau_P\).
時定数が小さいほど振動の周期が不安定で大きく暴れ、逆にあまり大きくとりすぎると変化があまりに緩やかで平衡に至るまでの時間がかかります。この辺りは熱浴法の時定数と同じ考え方です。力学的にfcc-Cuと類似の系に関しては体積変化の安定性と収束性から\(\tau_P\)は10\(^2\) fsから10\(^3\) fs付近が適切なようです。
次に\(\beta_T\)に対する依存性です。結果は以下のとおりです。
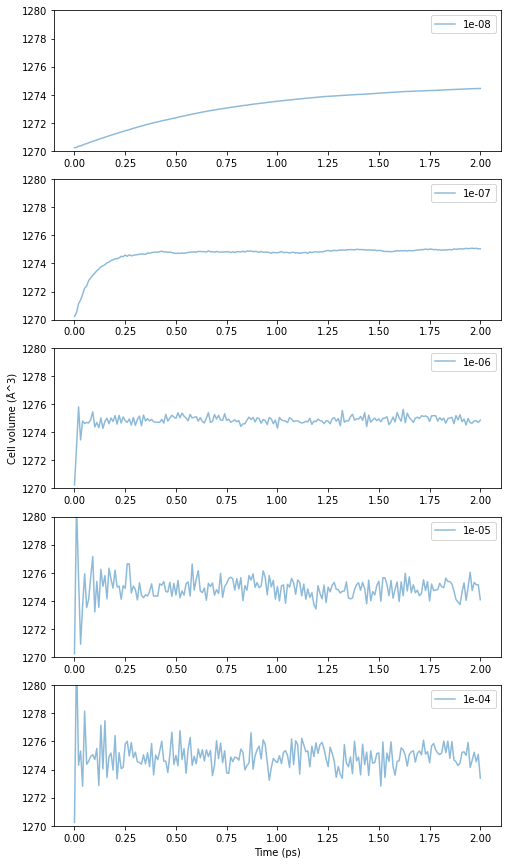
Fig.6-3e. Time evolution of cell volume as a function of \(\beta_T\).
\(\beta_T\)が小さいほど収束が非常に遅く、高い値にあるほど不安定になっていく様子がうかがえます。グラフの傾向から\(\beta_T\)は10\(^{-7}\)から10\(^{-6}\)fs位が良さそうです。
\(\tau_P\)と\(\beta_T\)に関してはいずれも厳密に正しい値というものは無く、おおよそ桁で値を変えた時にこの程度傾向が変化するということを理解しておけば概ね問題はなさそうです。
最後に補足すると、これらの数値はあくまでfcc-Cuのような金属で密な構造を持つ物質について適用出来ますが、もし全く異なる系統の物質(例えばポリマー、液体、気体等)をNPTで扱いたいとなれば事前検討でこれらの適切な値の領域を確認しておく必要があります。手間を惜しんで事前検討を省くと意図しない結果が得られて余計に時間がかかるなどになりかねないので、通常、新しい材料系に取り組む際は注意されることをお勧めします。
参考文献¶
[1] M.E. Tuckerman, “Statistical mechanics: Theory and molecular simulation”, Oxford University Press (2010) ISBN 978-0-19-852526-4. https://global.oup.com/academic/product/statistical-mechanics-9780198525264?q=Statistical%20mechanics:%20Theory%20and%20molecular%20simulation&cc=gb&lang=en#
[2] Melchionna S. (2000) “Constrained systems and statistical distribution”, Physical Review E 61 (6) 6165 https://journals.aps.org/pre/abstract/10.1103/PhysRevE.61.6165
[3] S. Melchionna, G. Ciccotti, B.L. Holian, “Hoover NPT dynamics for systems varying in shape and size”, Molecular Physics, (1993) 78 (3) 533 https://doi.org/10.1080/00268979300100371
[4] F.C. Nix, D. MacNair, “NIST:The Thermal Expansion of Pure Metals: Copper, Gold, Aluminum, Nickel, and Iron” https://materialsdata.nist.gov/handle/11256/32
[5] H. J. C. Berendsen, J. P. M. Postma, W. F. van Gunsteren, A. DiNola, and J. R. Haak, “Molecular dynamics with coupling to an external bath”, J. Chem. Phys. (1984) 81 3684 https://aip.scitation.org/doi/10.1063/1.448118