分子動力学シミュレーション¶
TL;DR¶
MDシミュレーションでは古典力学の運動方程式に則った計算方法で、全ての原子の位置と速度の時間発展を露わに観察できる。
時間スケールの制約があり一般的に数nsから数十nsぐらいが上限。その時間内に発現しない現象は別の計算手法を検討する必要がある。
MDシミュレーションには再現したい状態に応じて様々な状態(アンサンブル)があり、最も単純なアンサンブルはNVEアンサンブルという。
NVEアンサンブルでは全エネルギー保存則が成立し、計算精度および計算時間の観点から、時間ステップサイズを適切に設定する必要がある。
この章では系の時間発展をシミュレーションする、 分子動力学シミュレーション(Molecular dynamics, MD) について学びます。
MDシミュレーションでは個々の原子の軌道の時間発展を露わに取り扱うシミュレーションで、古典力学の運動方程式を積分することによって計算対象である原子の座標と速度を逐次計算していく手法です。この計算手法自体は原子間に働く力やエネルギーのモデルとは独立した理論で、古くから分子シミュレーションの分野で用いられてきました。従って、理論的な背景や事例等は多くの書籍や文献が多く存在するのでそれらを確認していただければと思います。(参考文献:[1-3]) 本チュートリアルではあくまでMatlantisを使って実践的にこれらの計算を実行するために必要な知識を習得するところが目的となっています。
早速ですが具体的な事例を通して、どんなことがMDシミュレーションで観察出来るかみてみましょう。
事前準備 - 必要なライブラリのインストール¶
本章ではところどころ、ASE上で簡易に利用できる古典力場であるASAP3のEMT力場を利用しています。古典力場であるため精度や用途はかなり限定的ですがシンプルかつ高速で実行可能なのでチュートリアルとして事例を示すには十分な機能を持っています。ちなみにASAP3-EMTで利用可能な元素はNi、Cu、Pd、Ag、Pt、Auとこれらの合金に限定されます。インストールの仕方は以下のとおりです。
[1]:
!pip install --upgrade asap3
Looking in indexes: https://pypi.org/simple, http://pypi.artifact.svc:8080/simple
Collecting asap3
Downloading asap3-3.13.7.tar.gz (855 kB)
━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━ 855.8/855.8 kB 65.4 MB/s eta 0:00:00
Installing build dependencies ... one
Getting requirements to build wheel ... done
Installing backend dependencies ... one
Preparing metadata (pyproject.toml) ... done
Requirement already satisfied: ase>=3.23.0 in /home/jovyan/.py311/lib/python3.11/site-packages (from asap3) (3.25.0)
Requirement already satisfied: numpy>=1.19.5 in /home/jovyan/.py311/lib/python3.11/site-packages (from ase>=3.23.0->asap3) (1.26.4)
Requirement already satisfied: scipy>=1.6.0 in /home/jovyan/.py311/lib/python3.11/site-packages (from ase>=3.23.0->asap3) (1.15.3)
Requirement already satisfied: matplotlib>=3.3.4 in /home/jovyan/.py311/lib/python3.11/site-packages (from ase>=3.23.0->asap3) (3.10.3)
Requirement already satisfied: contourpy>=1.0.1 in /home/jovyan/.py311/lib/python3.11/site-packages (from matplotlib>=3.3.4->ase>=3.23.0->asap3) (1.3.2)
Requirement already satisfied: cycler>=0.10 in /home/jovyan/.py311/lib/python3.11/site-packages (from matplotlib>=3.3.4->ase>=3.23.0->asap3) (0.12.1)
Requirement already satisfied: fonttools>=4.22.0 in /home/jovyan/.py311/lib/python3.11/site-packages (from matplotlib>=3.3.4->ase>=3.23.0->asap3) (4.58.2)
Requirement already satisfied: kiwisolver>=1.3.1 in /home/jovyan/.py311/lib/python3.11/site-packages (from matplotlib>=3.3.4->ase>=3.23.0->asap3) (1.4.8)
Requirement already satisfied: packaging>=20.0 in /home/jovyan/.py311/lib/python3.11/site-packages (from matplotlib>=3.3.4->ase>=3.23.0->asap3) (25.0)
Requirement already satisfied: pillow>=8 in /home/jovyan/.py311/lib/python3.11/site-packages (from matplotlib>=3.3.4->ase>=3.23.0->asap3) (11.2.1)
Requirement already satisfied: pyparsing>=2.3.1 in /home/jovyan/.py311/lib/python3.11/site-packages (from matplotlib>=3.3.4->ase>=3.23.0->asap3) (3.2.3)
Requirement already satisfied: python-dateutil>=2.7 in /home/jovyan/.py311/lib/python3.11/site-packages (from matplotlib>=3.3.4->ase>=3.23.0->asap3) (2.9.0.post0)
Requirement already satisfied: six>=1.5 in /home/jovyan/.py311/lib/python3.11/site-packages (from python-dateutil>=2.7->matplotlib>=3.3.4->ase>=3.23.0->asap3) (1.17.0)
Building wheels for collected packages: asap3
done
Created wheel for asap3: filename=asap3-3.13.7-cp311-cp311-linux_x86_64.whl size=4461488 sha256=8ef68bdc4c47a62e592d5d40598d3921480daf8f34de9a6d3b63d718ff1ec1b7
Stored in directory: /home/jovyan/.cache/pip/wheels/d1/8c/80/5aa8169f1b9773bb685620a4ce577adcd238f95b106ce06013
Successfully built asap3
Installing collected packages: asap3
Successfully installed asap3-3.13.7
[notice] A new release of pip is available: 24.0 -> 25.1.1
[notice] To update, run: pip install --upgrade pip
ASAP3-EMTに関する詳細はASAPのサイトをご確認ください。
MDシミュレーションでなにが出来るか¶
以下の事例では金属Al構造の溶融状態をMDシミュレーションで再現しています。ご存知の通りアルミニウムは我々がよく見かける物質で工業的に非常に重要な金属であり、その特性も良く知られています。融点は660.3 °C(933.45 K)で、常圧下では幅広い温度領域で面心立方格子(face-centered cubic, fcc)構造を持ちます。以下はそのfcc-Al構造を初期温度1600 Kに過熱して熔融させる過程を示したものです。計算時間は100 psecです。
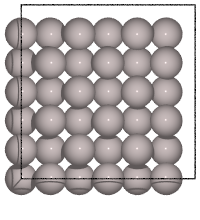
Fig6-1a. Melting of fcc-Al in NVE ensemble starting at 1600 K
(File: ../input/ch6/6-1_fcc-Al_NVE_1600Kstart.traj)
最初はきれいにfccの結晶構造に配置されたAl原子ですが、計算が進むにつれ徐々に構造が乱れ、段々とシミュレーションセルの外側に拡散していく様子がうかがえます。このようにMDシミュレーションでは実際に原子が時間発展とともにどのような軌道を描くか詳細に観察することが可能です。
アルミニウムの溶融シミュレーション¶
それでは以下に、上記のfcc-Alの溶融過程を再現するのに用いたMDシミュレーションのサンプルコードを示します。今回は計算の高速化のためASAP3のEMT力場を用いています。(ユーザーのpython環境でこの力場を用いる際は始めにpip install asap3を実行してasap3のパッケージをインストールしてください。)以下の計算は100 psec実行しますが、数十秒ほどで計算が完了します。
[2]:
%%time
import os
from asap3 import EMT
calculator = EMT()
from ase.build import bulk
from ase.md.velocitydistribution import MaxwellBoltzmannDistribution,Stationary
from ase.md.verlet import VelocityVerlet
from ase.md import MDLogger
from ase import units
from time import perf_counter
import numpy as np
# Set up a fcc-Al crystal
atoms = bulk("Al","fcc",a=4.3,cubic=True)
atoms.pbc = True
atoms *= 3
print("atoms = ",atoms)
# Set calculator (EMT in this case)
atoms.calc = calculator
# input parameters
time_step = 1.0 # MD step size in fsec
temperature = 1600 # Temperature in Kelvin
num_md_steps = 100000 # Total number of MD steps
num_interval = 1000 # Print out interval for .log and .traj
# Set the momenta corresponding to the given "temperature"
MaxwellBoltzmannDistribution(atoms, temperature_K=temperature,force_temp=True)
Stationary(atoms) # Set zero total momentum to avoid drifting
# Set output filenames
output_filename = "./output/ch6/liquid-Al_NVE_1.0fs_test"
log_filename = output_filename + ".log"
print("log_filename = ",log_filename)
traj_filename = output_filename + ".traj"
print("traj_filename = ",traj_filename)
# Remove old files if they exist
if os.path.exists(log_filename): os.remove(log_filename)
if os.path.exists(traj_filename): os.remove(traj_filename)
# Define the MD dynamics class object
dyn = VelocityVerlet(atoms,
time_step * units.fs,
trajectory = traj_filename,
loginterval=num_interval
)
# Print statements
def print_dyn():
imd = dyn.get_number_of_steps()
time_md = time_step*imd
etot = atoms.get_total_energy()
ekin = atoms.get_kinetic_energy()
epot = atoms.get_potential_energy()
temp_K = atoms.get_temperature()
print(f" {imd: >3} {etot:.9f} {ekin:.9f} {epot:.9f} {temp_K:.2f}")
dyn.attach(print_dyn, interval=num_interval)
# Set MD logger
dyn.attach(MDLogger(dyn, atoms, log_filename, header=True, stress=False,peratom=False, mode="w"), interval=num_interval)
# Now run MD simulation
print(f"\n imd Etot(eV) Ekin(eV) Epot(eV) T(K)")
dyn.run(num_md_steps)
print("\nNormal termination of the MD run!")
atoms = Atoms(symbols='Al108', pbc=True, cell=[12.899999999999999, 12.899999999999999, 12.899999999999999])
log_filename = ./output/ch6/liquid-Al_NVE_1.0fs_test.log
traj_filename = ./output/ch6/liquid-Al_NVE_1.0fs_test.traj
imd Etot(eV) Ekin(eV) Epot(eV) T(K)
0 32.139701294 22.336120234 9.803581060 1600.00
1000 32.144722159 9.393665122 22.751057037 672.90
2000 32.144501700 10.379779872 21.764721828 743.53
3000 32.144318649 10.246193775 21.898124875 733.96
4000 32.144092145 11.057828314 21.086263831 792.10
5000 32.144046250 11.951114265 20.192931985 856.09
6000 32.144260378 10.923214025 21.221046353 782.46
7000 32.144403860 10.881528388 21.262875472 779.47
8000 32.144603170 10.966654516 21.177948654 785.57
9000 32.144375218 11.119079419 21.025295799 796.49
10000 32.144222322 11.189498687 20.954723635 801.54
11000 32.144440573 9.685355360 22.459085213 693.79
12000 32.144344847 10.762266046 21.382078801 770.93
13000 32.144479122 8.902966113 23.241513009 637.74
14000 32.144045468 11.006792340 21.137253128 788.45
15000 32.144403754 10.902851629 21.241552125 781.00
16000 32.144707168 9.021035461 23.123671707 646.20
17000 32.144642186 10.023978285 22.120663901 718.05
18000 32.144529839 10.291094693 21.853435146 737.18
19000 32.144050744 11.312184244 20.831866500 810.32
20000 32.144890930 9.067681632 23.077209298 649.54
21000 32.143962314 11.384761628 20.759200686 815.52
22000 32.144291661 11.076124249 21.068167412 793.41
23000 32.144432732 10.505241125 21.639191607 752.52
24000 32.144434143 9.677110695 22.467323448 693.20
25000 32.144411792 10.096105345 22.048306447 723.21
26000 32.144418684 10.314244415 21.830174269 738.84
27000 32.144056137 10.819549400 21.324506737 775.04
28000 32.144136380 10.282863144 21.861273236 736.59
29000 32.144064247 10.603706988 21.540357259 759.57
30000 32.144142785 10.559098906 21.585043879 756.38
31000 32.144361966 9.657395222 22.486966744 691.79
32000 32.144754870 8.707546903 23.437207967 623.75
33000 32.144403555 10.326549807 21.817853748 739.72
34000 32.143748162 11.951159073 20.192589088 856.10
35000 32.144315603 10.100633141 22.043682462 723.54
36000 32.144494671 9.299422264 22.845072408 666.14
37000 32.144459312 10.264518196 21.879941116 735.28
38000 32.144381071 10.328971396 21.815409675 739.89
39000 32.143938348 10.560093761 21.583844587 756.45
40000 32.144102210 10.942980034 21.201122176 783.88
41000 32.144304063 9.758359111 22.385944952 699.02
42000 32.144112774 10.411570083 21.732542691 745.81
43000 32.144261663 11.015808525 21.128453137 789.09
44000 32.143624324 11.206493107 20.937131217 802.75
45000 32.143866741 10.944182507 21.199684234 783.96
46000 32.144367770 9.874633405 22.269734364 707.35
47000 32.143616353 11.287305027 20.856311326 808.54
48000 32.144377245 10.154501900 21.989875345 727.40
49000 32.144159709 10.059211532 22.084948176 720.57
50000 32.144028665 9.486133089 22.657895576 679.52
51000 32.143870407 10.461223944 21.682646463 749.37
52000 32.144010351 11.677881834 20.466128517 836.52
53000 32.143902994 11.086181772 21.057721222 794.13
54000 32.144209243 10.877133213 21.267076030 779.16
55000 32.143866159 11.672773150 20.471093009 836.15
56000 32.144245550 10.188169764 21.956075786 729.81
57000 32.144065429 10.540759442 21.603305987 755.06
58000 32.144047181 11.236293826 20.907753356 804.89
59000 32.144231273 10.845868548 21.298362725 776.92
60000 32.144175394 10.095420061 22.048755333 723.16
61000 32.144210124 10.751451533 21.392758591 770.16
62000 32.144358234 9.409524372 22.734833861 674.03
63000 32.144063044 10.947444309 21.196618735 784.20
64000 32.144231053 11.017702487 21.126528566 789.23
65000 32.144695236 9.546443148 22.598252088 683.84
66000 32.144162224 11.276822936 20.867339288 807.79
67000 32.144488062 10.519866599 21.624621463 753.57
68000 32.144557555 10.129716371 22.014841184 725.62
69000 32.144450322 10.284807689 21.859642633 736.73
70000 32.144447181 10.400649435 21.743797746 745.03
71000 32.144632289 9.627578409 22.517053880 689.65
72000 32.144341422 10.961964783 21.182376639 785.24
73000 32.144545573 10.711859413 21.432686160 767.32
74000 32.144810591 9.861638540 22.283172051 706.42
75000 32.144743025 10.142373359 22.002369665 726.53
76000 32.144666166 10.330929323 21.813736843 740.03
77000 32.145018460 9.962101343 22.182917118 713.61
78000 32.144948334 10.163190408 21.981757925 728.02
79000 32.144724224 10.841427576 21.303296648 776.60
80000 32.144567401 10.946160891 21.198406510 784.10
81000 32.144693558 10.170510668 21.974182891 728.54
82000 32.144802089 9.862497743 22.282304346 706.48
83000 32.145176925 9.213573320 22.931603605 659.99
84000 32.145220296 9.216727852 22.928492444 660.22
85000 32.145225359 8.782294025 23.362931334 629.10
86000 32.145009261 7.957304052 24.187705209 570.00
87000 32.144947628 8.411435060 23.733512568 602.54
88000 32.144898967 8.540565949 23.604333018 611.79
89000 32.145000371 8.278721461 23.866278910 593.03
90000 32.144782624 8.383947198 23.760835427 600.57
91000 32.145227363 8.091000385 24.054226978 579.58
92000 32.144911313 8.987582334 23.157328979 643.81
93000 32.145250110 7.310771383 24.834478726 523.69
94000 32.144846879 9.663598769 22.481248111 692.23
95000 32.145210301 8.115149170 24.030061131 581.31
96000 32.144906799 8.290101213 23.854805586 593.84
97000 32.144800583 7.827986525 24.316814058 560.74
98000 32.145024360 8.451294407 23.693729953 605.39
99000 32.144819857 8.631967805 23.512852051 618.33
100000 32.145028766 8.010498131 24.134530635 573.81
Normal termination of the MD run!
CPU times: user 25.6 s, sys: 203 ms, total: 25.8 s
Wall time: 25.6 s
プログラムの流れはスクリプト内のコメントを見ながら流れを追っていけばだいたい理解できるとは思いますが重要なポイントのみについて解説します。
(1)初速度分布
構造作成、計算パラメーターの設定が終わったのち、各原子の初速度は指定の温度に対応したMaxwell-Boltzmann分布に従う速度分布を与えます。上記コードでは、 MaxwellBoltzmannDistribution
を用いて行っています。この方法で与えた初速度には系全体の運動量の任意性があるため、このままでは系全体がドリフトする可能性があります。なのでMaxwell-BoltzmannDistributionで初速度を与えた後にStationaryという関数で系全体の運動量をゼロとし、質量中心の座標を固定します。NVEの事例だけでなく、この後出てくる温度制御や圧力制御を伴うシミュレーションでも重要になります。
(2)MDの実行
今回は、VelocityVerletというクラスを用いることで、速度ベルレ法によるMDを実行しています。 dyn.run(num_md_steps) の箇所で実際にMDの実行が行われています。 今回の設定では、time_step=1.0として、1stepあたり1fs = \(1 \times 10^{-15}\) secの時間幅で、num_md_steps=100000 step実行しています。
(3)計算結果の記録
このスクリプトにはprint_dynという標準出力(notebook上へのデータの出力)にエネルギーや温度の値を出力する関数があります。その他にもMDLoggerという関数があり、これは指定したLogファイルの中にエネルギー、温度、応力情報を出力します。独自に計算結果をファイル出力する機構を作っても良いですが、デフォルトで備わっているLoggerで大抵のアプリケーションに必要な情報は得られるので活用をお薦めします。
MD実行後、軌跡の可視化は以下のように行なえます。
[3]:
from ase.io import Trajectory
from pfcc_extras.visualize.view import view_ngl
traj = Trajectory(traj_filename)
view_ngl(traj)
[3]:
[4]:
from pfcc_extras.visualize.povray import traj_to_apng
from IPython.display import Image
traj_to_apng(traj, f"output/Fig6-1_fcc-Al_NVE_1600Kstart.png", rotation="0x,0y,0z", clean=True, n_jobs=16)
# See Fig6-1a
#Image(url="output/Fig6-1_fcc-Al_NVE_1600Kstart.png")
[Parallel(n_jobs=16)]: Using backend ThreadingBackend with 16 concurrent workers.
[Parallel(n_jobs=16)]: Done 18 tasks | elapsed: 12.8s
[Parallel(n_jobs=16)]: Done 101 out of 101 | elapsed: 41.7s finished
NVEアンサンブルにおける物性値のヒストリー¶
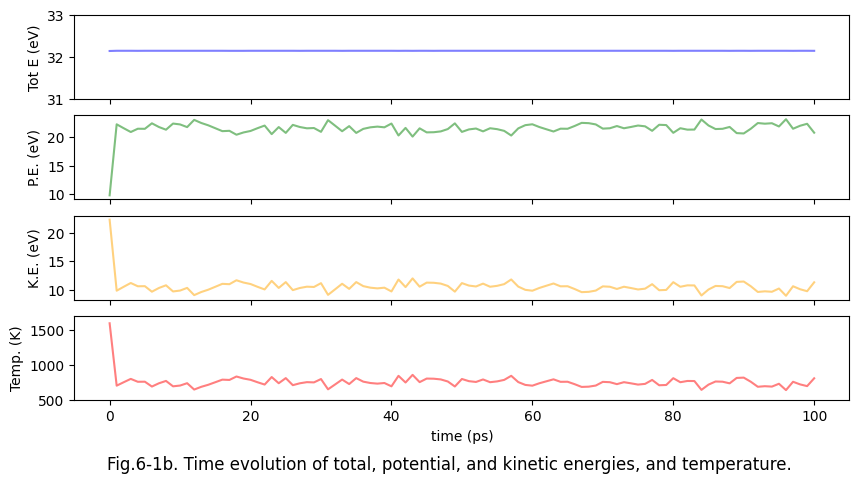
各原子の速度(すなわち運動量)も分かるため各種エネルギーの履歴を追うことも出来ます。例えば、以下は上のfcc-Alの溶融の際の全エネルギー(Tot.E.)、ポテンシャルエネルギー(P.E.)、運動エネルギー(K.E.)、そして温度(Temp.)の時間プロファイルです。
[5]:
import pandas as pd
df = pd.read_csv(log_filename, delim_whitespace=True)
df
/tmp/ipykernel_50921/510401485.py:3: FutureWarning: The 'delim_whitespace' keyword in pd.read_csv is deprecated and will be removed in a future version. Use ``sep='\s+'`` instead
df = pd.read_csv(log_filename, delim_whitespace=True)
[5]:
| Time[ps] | Etot[eV] | Epot[eV] | Ekin[eV] | T[K] | |
|---|---|---|---|---|---|
| 0 | 0.0 | 32.140 | 9.804 | 22.336 | 1600.0 |
| 1 | 1.0 | 32.145 | 22.751 | 9.394 | 672.9 |
| 2 | 2.0 | 32.145 | 21.765 | 10.380 | 743.5 |
| 3 | 3.0 | 32.144 | 21.898 | 10.246 | 734.0 |
| 4 | 4.0 | 32.144 | 21.086 | 11.058 | 792.1 |
| ... | ... | ... | ... | ... | ... |
| 96 | 96.0 | 32.145 | 23.855 | 8.290 | 593.8 |
| 97 | 97.0 | 32.145 | 24.317 | 7.828 | 560.7 |
| 98 | 98.0 | 32.145 | 23.694 | 8.451 | 605.4 |
| 99 | 99.0 | 32.145 | 23.513 | 8.632 | 618.3 |
| 100 | 100.0 | 32.145 | 24.135 | 8.010 | 573.8 |
101 rows × 5 columns
[6]:
import numpy as np
import matplotlib.pyplot as plt
fig = plt.figure(figsize=(10, 5))
#color = 'tab:grey'
ax1 = fig.add_subplot(4, 1, 1)
ax1.set_xticklabels([])
ax1.set_ylabel('Tot E (eV)')
ax1.set_ylim([31.,33.])
ax1.plot(df["Time[ps]"], df["Etot[eV]"], color="blue",alpha=0.5)
ax2 = fig.add_subplot(4, 1, 2)
ax2.set_xticklabels([])
ax2.set_ylabel('P.E. (eV)')
ax2.plot(df["Time[ps]"], df["Epot[eV]"], color="green",alpha=0.5)
ax3 = fig.add_subplot(4, 1, 3)
ax3.set_xticklabels([])
ax3.set_ylabel('K.E. (eV)')
ax3.plot(df["Time[ps]"], df["Ekin[eV]"], color="orange",alpha=0.5)
ax4 = fig.add_subplot(4, 1, 4)
ax4.set_xlabel('time (ps)')
ax4.set_ylabel('Temp. (K)')
ax4.plot(df["Time[ps]"], df["T[K]"], color="red",alpha=0.5)
ax4.set_ylim([500., 1700])
fig.suptitle("Fig.6-1b. Time evolution of total, potential, and kinetic energies, and temperature.", y=0)
#plt.savefig("6-1_liquid-Al_NVE_1.0fs_test_E_vs_t.png") # <- Use if saving to an image file is desired
plt.show()
1-5節 でも出てきましたが、系の全エネルギー \(E\) (Total energy) は、運動エネルギー \(K\) (Kinetic energy)と、ポテンシャルエネルギー \(V\) (Potential energy)で表されます。
このうち、原子の運動エネルギー\(K\)は古典力学の表式を用い以下のように計算できます。
ここで \(m_i, \mathbf{v}_i, \mathbf{p}_i\) はそれぞれ各原子の質量 (mass) 、速度 (velocity)および運動量 (momenta, \(\mathbf{p}=m\mathbf{v}\))です。ここで系の温度と運動エネルギーはほぼ同義で、以下のような関係で定義されます。
今回のケースでは初期温度を1600 Kと設定し、あとは古典力学の運動方程式に則って自然に系を時間発展させています。従って特に外力もないのでエネルギー保存則が守られ全エネルギーが数値誤差の範囲で一定に保たれます。そしてかなり早い段階で温度が低下し、運動エネルギーとポテンシャルエネルギーのそれぞれにエネルギー分配則が働き、最終的に温度は初期温度の半分程度に落ち着きます。自然界では実際に物質はそのようにふるまい、今回のような最もシンプルなMDシミュレーションではそういった状況を再現します。このような計算対象である系の状態分布をNVEアンサンブルと言います。(または小正準集団アンサンブル。NVEのNは原子数、Vは体積、Eは全エネルギーが一定であることを表します。)ちなみに、ここでいうアンサンブルとは統計力学の考え方で物質の状態分布のことを指します。
NVEアンサンブルにおけるMDシミュレーションの設定¶
さて、上記のNVEアンサンブルのMDシミュレーションでは初期温度や計算時間のような計算条件を設定する必要があります。それ以外にも比較的自明ではないパラメーターとしてMDのタイムステップを設定する必要があります。このMDのタイムステップはどのように設定したらよいでしょうか?
答えは求めている計算精度に依存します。NVEアンサンブルでは2階の常微分方程式である古典の運動方程式解くわけですが、この積分プロセスの精度がタイムステップの大きさで決まります。(積分手法の詳細については本節の最後に記載します。)タイムステップサイズを変えた時の全エネルギーがどのように変化するか見てみましょう。計算時間は仮に1 nsecとします。(古典MDなどで良く用いられる時間スケールです。)
Fig.6-1c. Time evolution of the total energy with respect to time step size.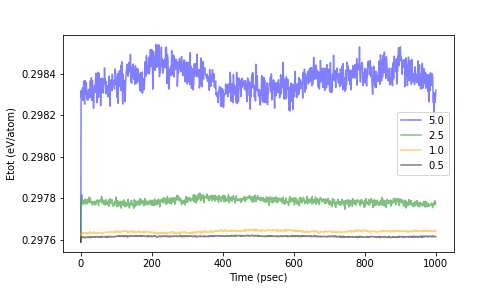
上記はタイムステップを0.5から5.0 fsecまで変化させたときの計算結果です。本来一定であるはずの全エネルギーが、タイムステップが大きいときに時間の経過とともに大きくぶれてしまっていることが確認できます。
全エネルギーの時間依存性確認のため、上記のMDシミュレーションスクリプトのtime_step 引数を変えて実行し、そのエネルギープロファイルを比較してみてください。 可視化にあたっては、上記Fig.6-1b の可視化コードを参考にしてください。
上記の計算結果からMDのタイムステップサイズを変化し、横軸をステップサイズ、縦軸を全エネルギーの揺らぎから得られたRMSEをプロットすると以下のようになります。
Fig.6-1d. Total energy ERMSE as a function of MD step size.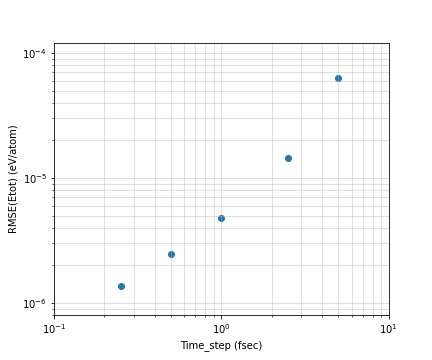
縦軸は原子ひとつ辺りのエネルギーです。Log-logプロットで概ね直線上にのることが見て取れます。単位原子当たりの値にして、0.25 fsで1.2e-6 eVから5.0 fsで6e-5 fsまで変化することが分かります。この場合原子数は108原子なので、系全体で1e-4 eVから1e-3 eV変化しうることが確認できます。
エネルギーの観点では時間ステップを1 fsecとすると、1 nsecのシミュレーションを100原子系で0.5 meV程度、1000原子系だと約5 meV程度の誤差が予想されます。もちろん計算したい物性などによりますが、たいていの計算では十分な精度ではないでしょうか?これが例えば計算時間を稼ぎたいからとタイムステップを5 fsecとするとほぼ一桁誤差が大きくなります。今後MD計算を活用するうえで、この計算精度がどの程度かというのは頭の片隅に止めておく必要があります。
その他のアンサンブルとMDシミュレーション¶
本節の最後にNVEアンサンブル以外のMDシミュレーション法について触れておきます。
NVEアンサンブルのMDシミュレーションはシンプルかつパワフルな計算手法ですが、我々が一般に観察したい現象を再現するには不都合な点が多く存在します。 NVEのシミュレーションは計算対象のセルそれそのものが全てであり、外界というものが存在しません。しかし我々が実際に観察したいミクロな世界にはそれを取り巻く環境が存在します。外部環境の温度や圧力の影響により、計算対象の状態が変化しますが、これはNVEアンサンブルの範疇では再現が出来ません。
このため統計力学の世界ではcanonicalアンサンブル(NVT)、isothermal-isobaricアンサンブル(NPT)、等をはじめ様々な状態分布があり、それらを活用することで特定の条件下での計算が可能になります。次節以降ではこれらの統計力学アンサンブル下での計算方法について学びます。
参考文献¶
[1] M.P. Allen and D.J. Tildesley, “Computer simulaiton of liquid”, 2nd Ed., Oxford University Press (2017) ISBN 978-0-19-880319-5. DOI:10.1093/oso/9780198803195.001.0001
[2] D. Frenkel and B. Smit “Understanding molecular simulation - from algorithms to applications”, 2nd Ed., Academic Press (2002) ISBN 978-0-12-267351-1. DOI:10.1016/B978-0-12-267351-1.X5000-7
[3] M.E. Tuckerman, “Statistical mechanics: Theory and molecular simulation”, Oxford University Press (2010) ISBN 978-0-19-852526-4. https://global.oup.com/academic/product/statistical-mechanics-9780198525264?q=Statistical%20mechanics:%20Theory%20and%20molecular%20simulation&cc=gb&lang=en#